$k$-abelian singletons and Gray codes for Necklaces
Also appears in collection : Combinatorics on words / Combinatoire des mots
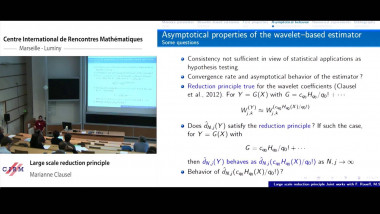
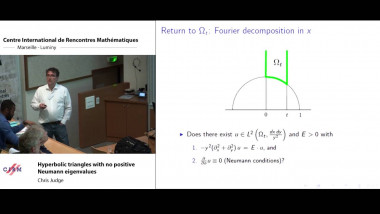
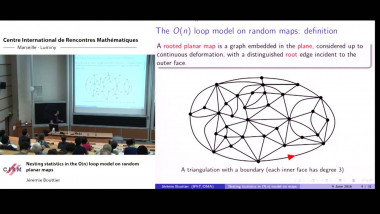
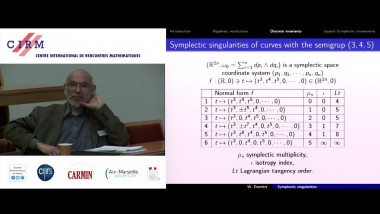
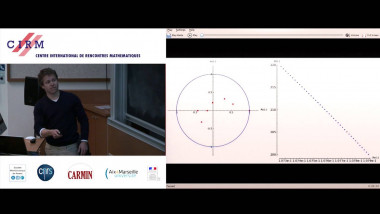
$k$-abelian singletons in connection with Gray codes for Necklaces. This work is based on [1]. We are interested in the equivalence classes induced by $k$-abelian equivalence, especially in the number of the classes containing only one element, $k$-abelian singletons. By characterizing $k$-abelian equivalence with $k$-switchings, a sort of rewriting operation, we are able to obtain a structural representation of $k$-abelian singletons. Analyzing this structural result leads, through rather technical considerations, to questions of certain properties of sets of vertex-disjoint cycles in the de Bruijn graph $dB_\Sigma(k-1)$ of order $k-1$. Some problems turn out to be equivalent to old open problems such as Gray codes for necklaces (or conjugacy classes). We shall formulate the problem in the following. Let $\mathcal{C} = \lbrace V_1, . . . , V_n\rbrace$ be a cycle decomposition of $dB_\Sigma(n)$, that is, a partition of the vertex set $\Sigma^n$ into sets, each inducing a cycle or a loop in $dB_\Sigma(n)$. Let us then define the quotient graph $dB_\Sigma/\mathcal{C}$ as follows. The set of points are the sets in $\mathcal{C}$. For distinct sets $X, Y \in \mathcal{C}$, we have and edge from $X$ to $Y$ if and only if there exists $x{\in}X,y{\in}Y$ such that $(x,y){\in}dB_\Sigma(n)$. An old result shows that the size of a cycle decomposition of $dB_\Sigma(n)$ is at most the number of necklaces of length $n$ over $\Sigma$ (see [2]). We call a cycle decomposition maximal, if its size is maximal. In particular, the cycle decomposition given by necklaces is maximal. Conjecture 1. For any $\Sigma$ and $n{\in}\mathbb{N}$, there exist a maximal cycle decomposition $\mathcal{C}$ of $dB_\Sigma(n)$ such that $dB_\Sigma(n)/\mathcal{C}$ contains a hamiltonian path. A natural candidate to study here is the cycle decomposition given by necklaces. This has been studied in the literature in the connection of Gray codes for necklaces. Concerning this, there is an open problem since $1997$ $[3]$ : Let $\Sigma = \lbrace0, 1\rbrace$, $n$ odd, and $\mathcal{C}$ be the cycle decomposition given by necklaces of length $n$ over $\lbrace0,1\rbrace$. Does $dB(n)/\mathcal{C}$ contain a hamiltonian path ? The answer to the above has been verified to be ”yes” for $n \le 15$ $([1]$). The case of $n \ge 4$ and $n$ even, the graph is bipartite with one partition larger than the other. On the other hand, we can find other maximal cycle decompositions of $dB_\Sigma(4)$, $dB_\Sigma(6)$, and $dB_\Sigma(8)$ for the binary alphabet which all admit hamiltonian quotient graphs. We concluded in $[1]$ that Conjecture $1$ is equivalent to the following $\Theta$-estimation of the number of $k$-abelian singletons of length $n$. Conjecture 2. The number of $k$-abelian singletons of length $n$ over alphabet $\Sigma$ is of order $\Theta(n^{N_{\Sigma}(k-1)-1})$, where $N_\Sigma(l)$ is the number of necklaces of length $l$ over $\Sigma$.

























































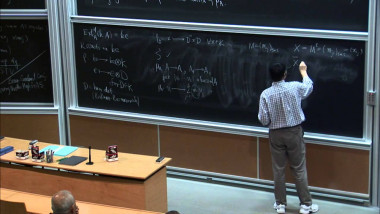


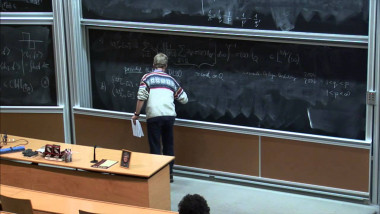

















































![$k$-sum free sets in $[0,1]$](/media/cache/video_light/uploads/video/2015-09-10_de_Roton-video--19cf70874d3c5af7378c268cab865b06.jpg)