A derivation on the field of d.c.e.reals
Also appears in collection : Computability, randomness and applications / Calculabilité, hasard et leurs applications
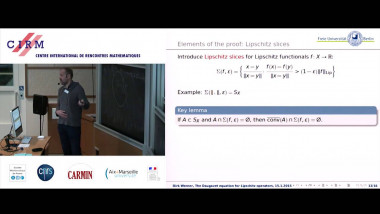
Barmpalias and Lewis-Pye recently proved that if $\alpha$ and $\beta$ are (Martin-Löf) random left-c.e. reals with left-c.e. approximations $\{\alpha_s }_{s \in\ omega}$ and $\{\beta_s }_{s \in\ omega}$, then [ \begin{equation} \frac{\partial\alpha}{\partial\beta} = \lim_{s\to\infty} \frac{\alpha-\alpha_s}{\beta-\beta_s}. \end{equation} ] converges and is independent of the choice of approximations. Furthermore, they showed that $\partial\alpha/\partial\beta = 1$ if and only if $\alpha-\beta$ is nonrandom; $\partial\alpha/\partial\beta>1$ if and only if $\alpha-\beta$ is a random left-c.e. real; and $\partial\alpha/\partial\beta<1$ if and only if $\alpha-\beta$ is a random right-c.e. real.
We extend their results to the d.c.e. reals, which clarifies what is happening. The extension is straightforward. Fix a random left-c.e. real $\Omega$ with approximation $\{\Omega_s}_{s\in\omega}$. If $\alpha$ is a d.c.e. real with d.c.e. approximation $\{\alpha_s}_{s\in\omega}$, let [ \partial\alpha = \frac{\partial\alpha}{\partial\Omega} = \lim_{s\to\infty} \frac{\alpha-\alpha_s}{\Omega-\Omega_s}. ] As above, the limit exists and is independent of the choice of approximations. Now $\partial\alpha=0$ if and only if $\alpha$ is nonrandom; $\partial\alpha>0$ if and only if $\alpha$ is a random left-c.e. real; and $\partial\alpha<0$ if and only if $\alpha$ is a random right-c.e. real.
As we have telegraphed by our choice of notation, $\partial$ is a derivation on the field of d.c.e. reals. In other words, $\partial$ preserves addition and satisfies the Leibniz law: [ \partial(\alpha\beta) = \alpha\,\partial\beta + \beta\,\partial\alpha. ] (However, $\partial$ maps outside of the d.c.e. reals, so it does not make them a differential field.) We will see how the properties of $\partial$ encapsulate much of what we know about randomness in the left-c.e. and d.c.e. reals. We also show that if $f\colon\mathbb{R}\rightarrow\mathbb{R}$ is a computable function that is differentiable at $\alpha$, then $\partial f(\alpha) = f'(\alpha)\,\partial\alpha$. This allows us to apply basic identities from calculus, so for example, $\partial\alpha^n = n\alpha^{n-1}\,\partial\alpha$ and $\partial e^\alpha = e^\alpha\,\partial\alpha$. Since $\partial\Omega=1$, we have $\partial e^\Omega = e^\Omega$.
Given a derivation on a field, the elements that it maps to zero also form a field: the $ \textit {field of constants}$. In our case, these are the nonrandom d.c.e. reals. We show that, in fact, the nonrandom d.c.e. reals form a $ \textit {real closed field}$. Note that it was not even known that the nonrandom d.c.e. reals are closed under addition, and indeed, it is easy to prove the convergence of [1] from this fact. In contrast, it has long been known that the nonrandom left-c.e. reals are closed under addition (Demuth [2] and Downey, Hirschfeldt, and Nies [3]). While also nontrivial, this fact seems to be easier to prove. Towards understanding this difference, we show that the real closure of the nonrandom left-c.e. reals is strictly smaller than the field of nonrandom d.c.e. reals. In particular, there are nonrandom d.c.e. reals that cannot be written as the difference of nonrandom left-c.e. reals; despite being nonrandom, they carry some kind of intrinsic randomness.












































































































![$k$-sum free sets in $[0,1]$](/media/cache/video_light/uploads/video/2015-09-10_de_Roton-video--19cf70874d3c5af7378c268cab865b06.jpg)