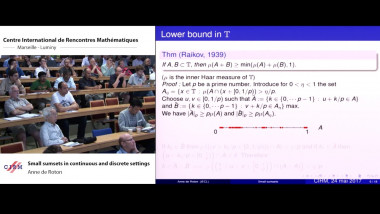
On a difference between two methods of low-distortion embeddings of finite metric spaces into non-superreflexive Banach spaces
Also appears in collection : Non linear functional analysis / Analyse fonctionnelle non linéaire
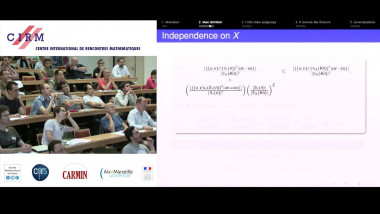
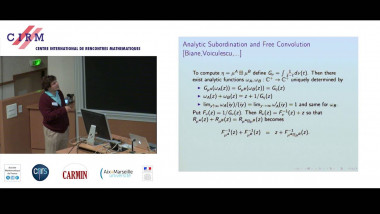
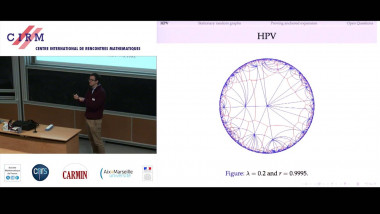
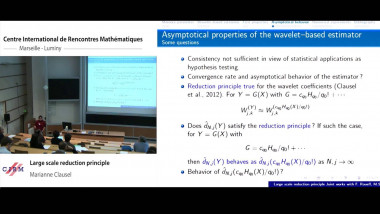
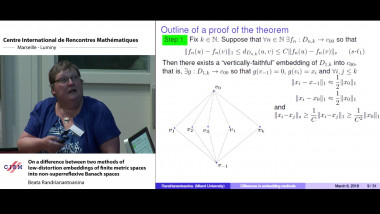
In a recent paper, the speaker and M.I. Ostrovskii developed a new metric embedding method based on the theory of equal-signs-additive (ESA) sequences developed by Brunel and Sucheston in 1970’s. This method was used to construct bilipschitz embeddings of diamond and Laakso graphs with an arbitrary finite number of branches into any non-superreflexive Banach space with a uniform bound on distortions that is independent of the number of branches. In this talk we will outline a proof that the above mentioned embeddability results cannot be obtained using the embedding method which was used for trees by Bourgain (1986) and for binary branching diamonds and Laakso graphs by Johnson and Schechtman (2009), and which is based on a classical James’ characterization of superreflexivity (the factorization between the summing basis and the unit vector basis of $\ell_1$). Our proof uses a “self-improvement” argument and the Ramsey theorem. Joint work with M.I. Ostrovskii.












































































































![$k$-sum free sets in $[0,1]$](/media/cache/video_light/uploads/video/2015-09-10_de_Roton-video--19cf70874d3c5af7378c268cab865b06.jpg)