Small Scale Index Theory, Scalar Curvature, and Gromov’s Simplicial Norm
By Qiaochu Ma
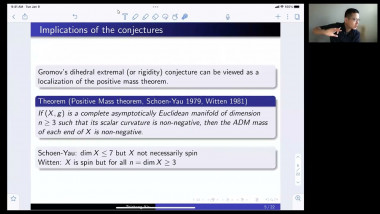
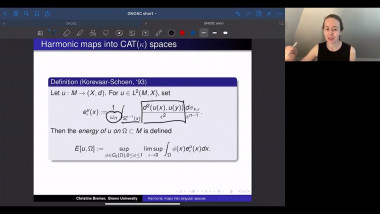
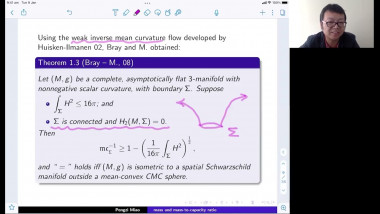
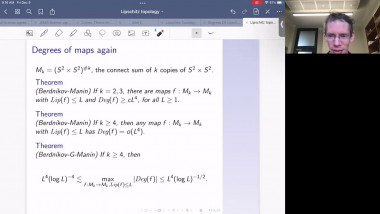
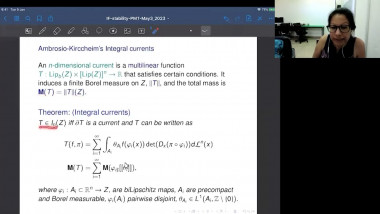
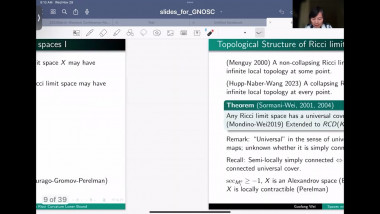
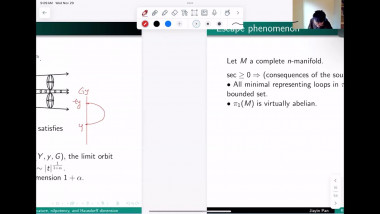
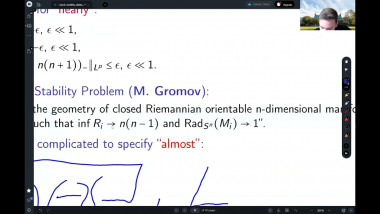
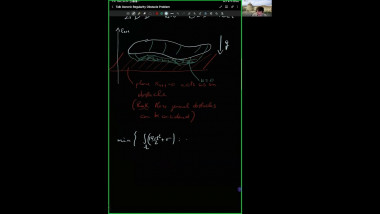
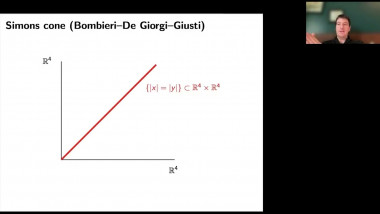
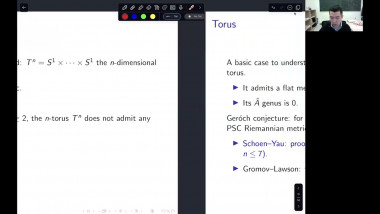
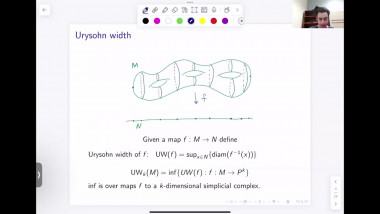
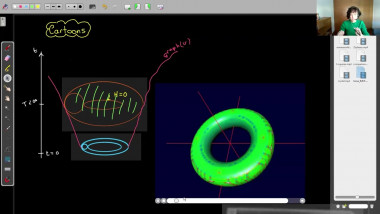
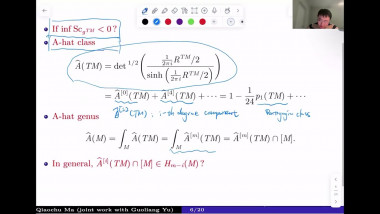
Scalar curvature encodes the volume information of small geodesic balls within a Riemannian manifold, making it, to some extent, the weakest curvature invariant. This raises a natural question: what topological constraints does scalar curvature impose on manifolds? In this talk, we shall show that for a manifold with a scalar curvature lower bound (possibly negative), the simplicial norm of the Poincaré dual of the A-hat class can be controlled. This is joint work with Guoliang Yu.