Quasi-local mass and geometry of scalar curvature
By Yuguang Shi
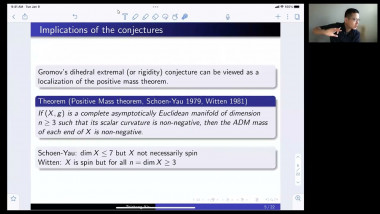
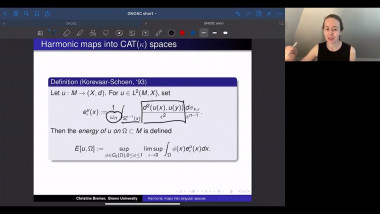
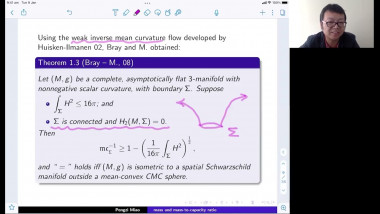
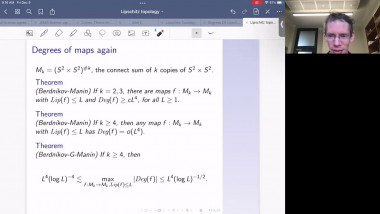
Quasi-local mass is a basic notion in General Relativity. Geometrically, it can be regarded as a geometric quantity of a boundary of a 3-dimensional compact Riemannian manifold. Usually, it is in terms of area and mean curvature of the boundary. It is interesting to see that some of quasi-local masses, like Brown-York mass, have deep relation with Gromov’s fill-in problem of metrics with scalar curvature bounded below. In this talk, I will discuss these relations. This talk is based on some of my recent joint works with J.Chen, P.Liu, W.L. Wang , G.D.Wei and J. Zhu etc.



































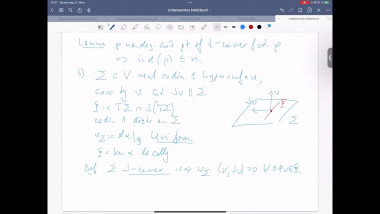

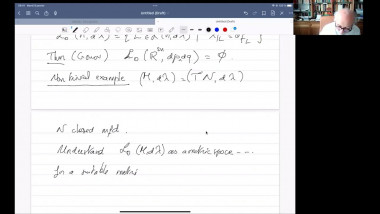

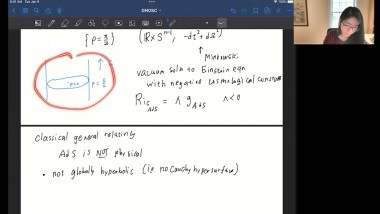
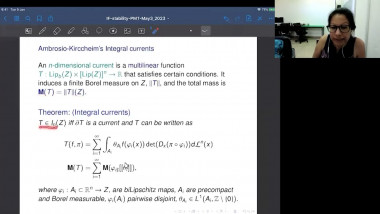








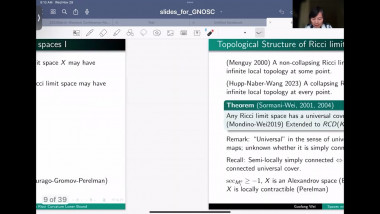
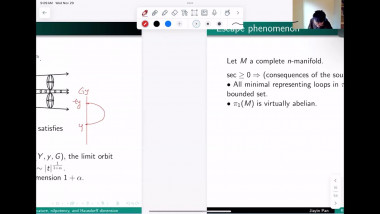
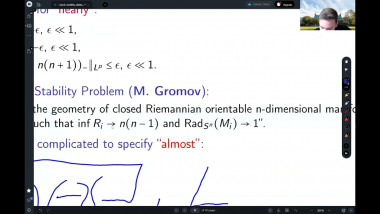

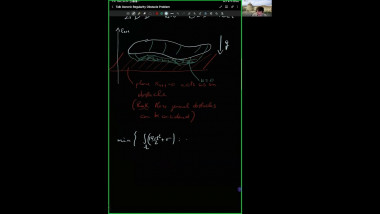
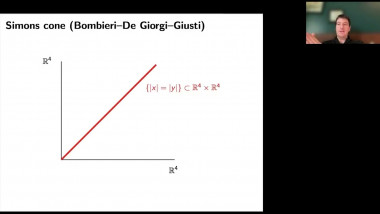




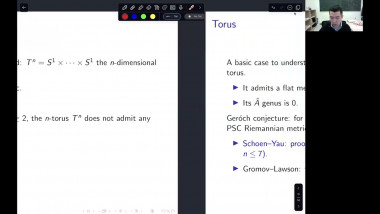




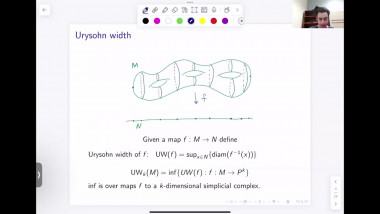







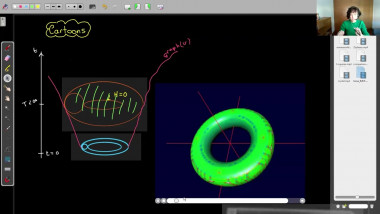




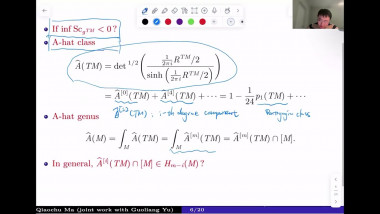






![[1247] Dérivation de l'équation de Boltzmann en temps long à partir d'une dynamique de sphères dures](/media/cache/video_light/uploads/video/SeminaireBourbaki.png)
