
Geometrical finiteness in strictly convex projective geometry
By Pierre-Louis Blayac
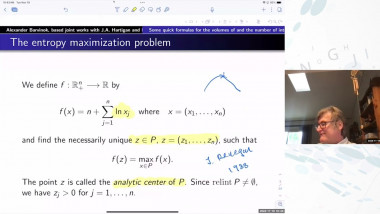
Some Quick Formulas for the Volumes of and the Number of Integer Points in Higher-dimensional Polyhedra
By Alexander Barvinok

Branching in Planar Optimal Transport and Positive Definite Functions
By Fyodor Petrov












