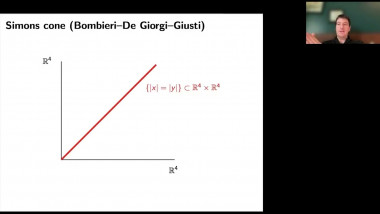
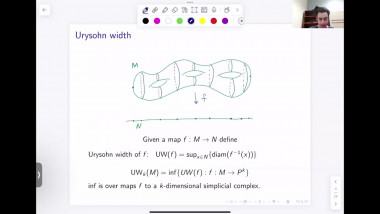
Lipschitz constant and degree of mappings
By Larry Guth
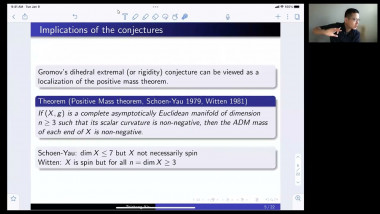
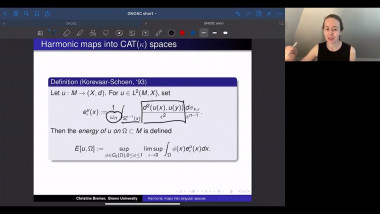
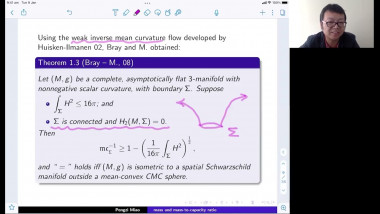
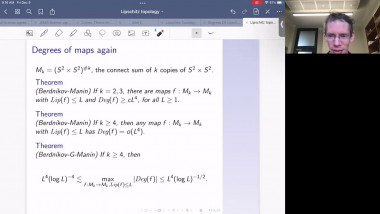
We will survey the connection between the Lipschitz constant of a map $f$ (between Riemannian manifolds) and the topological type of the map. We will mostly focus on the degree of the map, because the story is already quite complex in that case. If $f\colon M^n \to M^n$ has Lipschitz constant $L$, then the degree of $f$ is at most $L^n$. When $M$ is $S^n$, there are self maps with Lipschitz constant $L$ and degree at least $c_n L^n$. But what happens for other manifolds? We will survey recent developments on this question by Aleksandr Berdnikov and Fedor Manin. We will see some clever maps that are somewhat related to the maps Robert will talk about in the following talk.