A stable version of Gromov’s angle-shrinking problem and its index theoretic applications (Part I)
By Zhizhang Xie
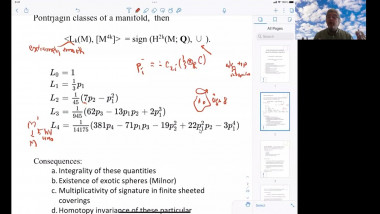
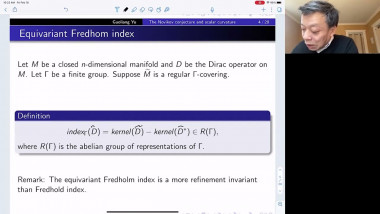
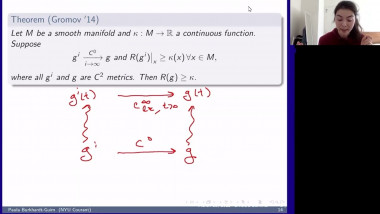
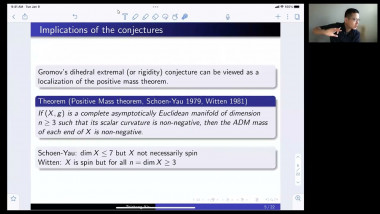
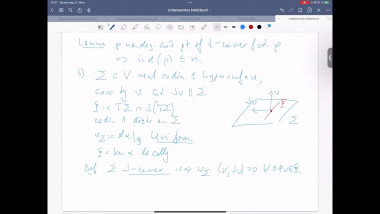
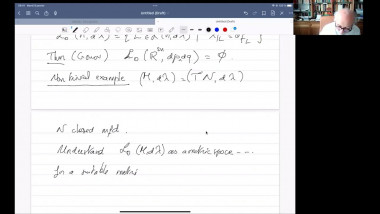
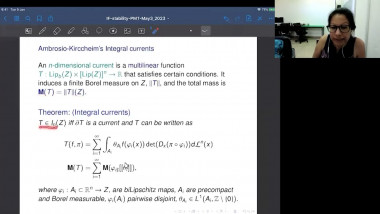
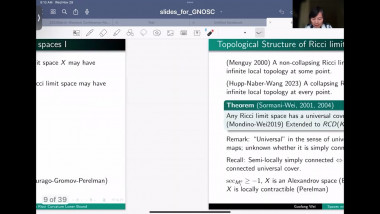
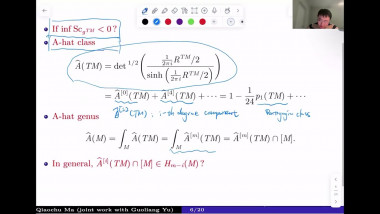
In this talk, we will discuss Gromov’s angle shrinking problem and how it enters into our proof of Gromov’s dihedral extremality/rigidity conjecture. More precisely, we proved Gromov’s dihedral extremality/rigidity conjecture via a new index theorem for manifolds with polyhedral boundary. One of main steps of the proof of this new index theorem is to compute the Fredholm index of a relevant Dirac type operator (with appropriate boundary conditions) on a polyhedral corner. A key ingredient of our proof is a deformation technique that allows us to reduce the computation of the Fredholm index to a model case where the computation becomes more or less straightforward. The deformation technique relies on a version of Gromov’s angle shrinking problem. While the original Gromov’s angle shrinking problem is still open, fortunately our deformation technique only requires a stable and algebraic version of Gromov’s angle shrinking problem, which turns out to be true in general. We will introduce this stable and algebraic version of Gromov’s angle shrinking problem, and explain how it is used in the proof of our index theorem. The talk is based on joint work with Jinmin Wang and Guoliang Yu.