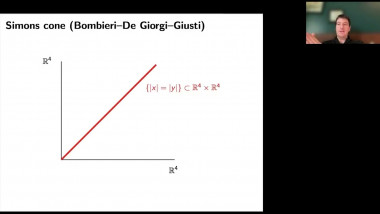
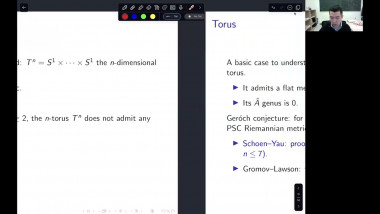
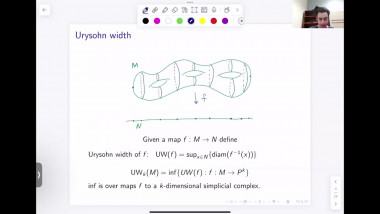
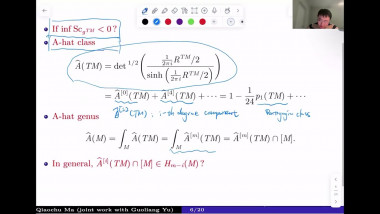
Regularising manifolds using Ricci flow
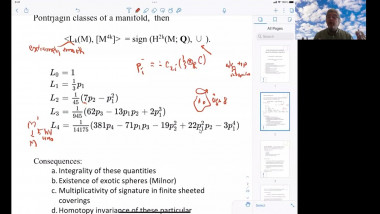
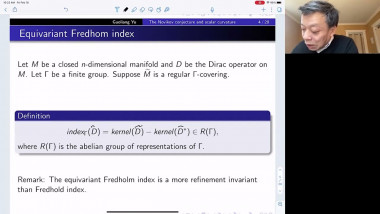
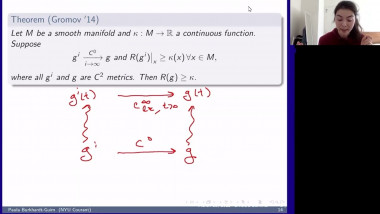
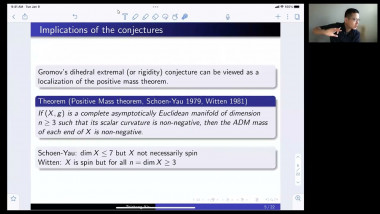
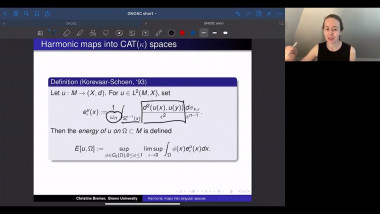
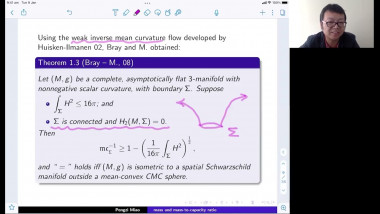
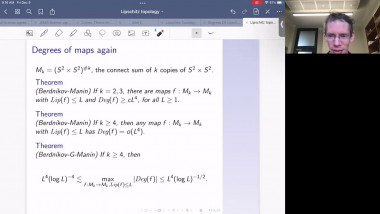
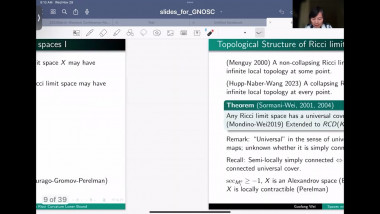
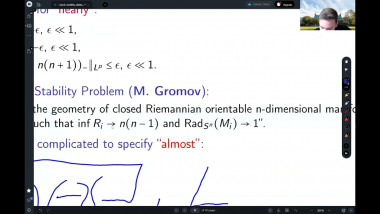
Ricci flow has proved its worth as a way of deforming a manifold satisfying geometric or topological conditions into very special manifolds that can be identified. For example, manifolds satisfying certain positive curvature conditions will be deformed to spherical space forms, allowing us to identify their topology. In this talk I will give a partial survey of other ways that Ricci flow has been used recently, focussing on applications that use its regularisation effect. For example, one can show that certain metric limit spaces are manifolds using this idea. Other applications include regularising the geometry of a manifold at infinity in order to prove pinching theorems, or finding new expanding Ricci solitons. I will pick one or two examples to explain.