Not Only Scalar Curvature Seminar

Collection Not Only Scalar Curvature Seminar

00:00:00 / 00:00:00

80 80

Application of Curvature Comparison Theorems in Minimal Surfaces

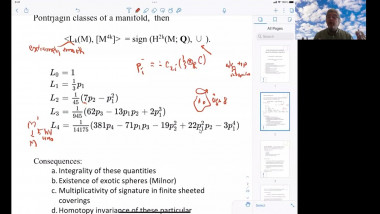
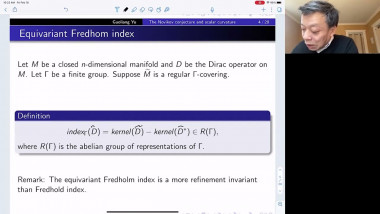
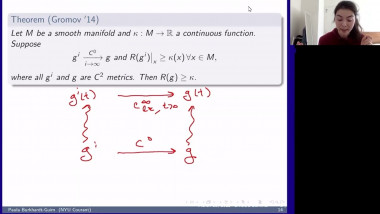
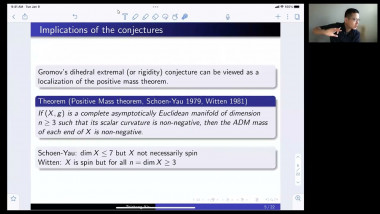
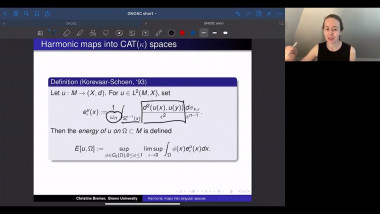
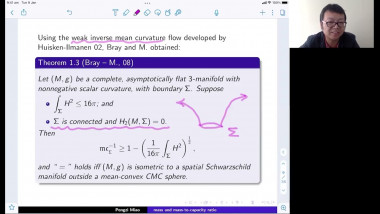
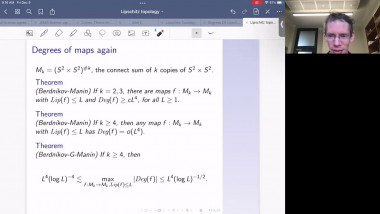
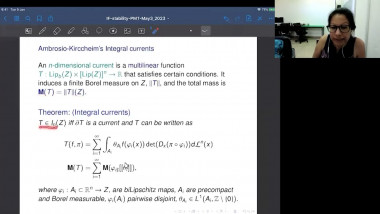
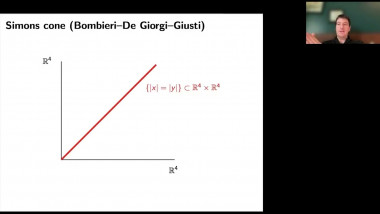
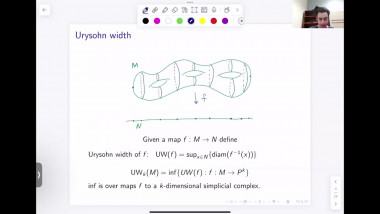
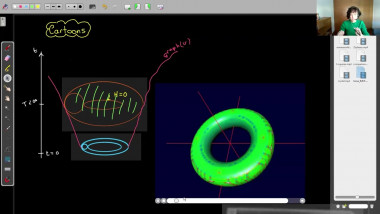
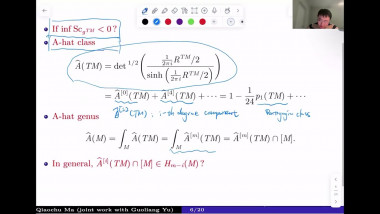
We use generalized minimal or capillary hypersurfaces to study comparison theorems of certain class of positively curved manifolds (with boundary); this is also called Gromov's $\mu$-bubble method. We apply these results to obtain useful geometric bounds such as Urysohn width, bandwidth estimates, and study rigidity of (free boundary) minimal hypersurfaces.

Information about the video

Date of recording 03/12/2025
Date of publication 05/12/2025
Institution IHES
Language English
Audience Researchers
Format MP4

Domain(s)

Differential Geometry

Last related questions on MathOverflow

You have to connect your Carmin.tv account with mathoverflow to add question

Ask a question on MathOverflow

All the collection videos

46:29

published on February 3, 2022

Invitation to scalar curvature

By Mikhail Gromov

01:02:05

published on February 3, 2022

Scalar and mean curvature comparison via the Dirac operator

By Rudolf Zeidler

49:31

published on February 25, 2022

Sequences of manifolds with lower bounds on their scalar curvature

By Christina Sormani

51:51

published on February 25, 2022

Scalar curvature and the dihedral rigidity conjecture

By Chao Li

49:38

published on February 22, 2022

Some introductory remarks on the Novikov conjecture

By Shmuel Weinberger

59:45

published on February 22, 2022

The Novikov conjecture and scalar curvature

By Guoliang Yu

54:54

published on March 11, 2022

Rigidity theorems for the diffeomorphism action on spaces of metrics of positive scalar curvature

By Johannes Ebert

44:46

published on March 11, 2022

Surgery, bordism and scalar curvature

By Bernhard Hanke

47:18

published on March 25, 2022

Ricci flow and singularities

By Natasa Sesum

52:49

published on March 25, 2022

Lower scalar curvature bounds for $C^0$ metrics: a Ricci flow approach

By Paula Burkhardt-Guim

59:42

published on April 7, 2022

Gromov’s dihedral rigidity conjecture and index theory on manifolds with corners

By Jinming Wang

01:01:04

published on April 7, 2022

Comparison of scalar curvature, mean curvature and dihedral angles, and their applications

By Zhizhang Xie

45:07

published on April 19, 2022

Deformations of Dirac operators

By Weiping Zhang

43:37

published on April 21, 2022

Nonnegative scalar curvature and area decreasing maps on complete foliated manifolds

By Guangxiang Su

44:57

published on May 3, 2022

Quasi-local mass and geometry of scalar curvature

By Yuguang Shi

01:03:49

published on May 3, 2022

Incompressible hypersurface, positive scalar curvature and positive mass theorem

By Jintian Zhu

43:08

published on May 11, 2022

Boundary value problems for Dirac operators

By Christian Bär

01:04:17

published on May 11, 2022

Distance estimates in the spin setting and the positive mass theorem

By Simone Cecchini

48:01

published on May 24, 2022

Yamabe constants, Yamabe invariants, and Gromov-Lawson surgeries

By Bernd Ammann

01:10:21

published on May 24, 2022

Yamabe invariants, Weyl curvature, and the differential topology of 4-manifolds

By Claude LeBrun

47:01

published on June 30, 2022

Harmonic maps to metric spaces and applications

By Christine Breiner

47:22

published on June 30, 2022

Level set methods for scalar curvature on three-manifolds

By Daniel Stern

59:15

published on November 14, 2022

Capacity in low regularity, with connections to general relativity

By Jeff Jauregui

47:02

published on November 3, 2022

Recent inequalities on the mass-to-capacity ratio

By Pengzi Miao

45:55

published on November 17, 2022

Scalar curvature rigidity and extremality in dimension 4

By Renato Bettiol

47:42

published on November 17, 2022

Scalar curvature rigidity

By Thomas Schick

52:09

published on December 30, 2022

Lipschitz constant and degree of mappings

By Larry Guth

57:53

published on December 30, 2022

Self-similar solutions to extension and approximation problems

By Robert Young

55:22

published on February 10, 2023

Currents on metric spaces and intrinsic flat convergence

By Christina Sormani

01:00:01

published on February 10, 2023

Spherical Plateau problem and applications

By Antoine Song

47:01

published on February 21, 2023

Recent developments in constant mean curvature hypersurfaces I

By Xin Zhou

51:23

published on February 21, 2023

Recent developments in constant mean curvature hypersurfaces II

By Liam Mazurowski

49:57

published on March 28, 2023

Stein and Weinstein manifolds

By Kai Cieliebak

01:02:35

published on March 28, 2023

Interplay between notions of convexity in complex, symplectic and contact geometries

By Yakov Eliashberg

48:07

published on April 27, 2023

The completion of the space of Lagrangian submanifolds for the spectral metric

By Claude Viterbo

59:02

published on April 27, 2023

A higher dimensional generalization of the Birkhoff attractor

By Vincent Humilière

51:59

published on May 31, 2023

Positive mass theorem for asymptocially hyperbolic manifolds

By Lan-Hsuan Huang

53:07

published on May 31, 2023

Intrinsic flat stability of the positive mass theorem for graphical manifolds

By Raquel Perales

01:11:26

published on June 13, 2023

Smoothing by Ricci-DeTurck flow and applications to scalar curvature

By Man-Chun Lee

46:38

published on June 13, 2023

Regularising manifolds using Ricci flow

By Peter Topping

49:06

published on November 14, 2023

Index theory and applications to scalar curvature

By Christian Bär

58:32

published on November 14, 2023

On Gromov’s rigidity theorem for polytopes with acute angles

By Yipeng Wang

55:50

published on November 14, 2023

Intrinsic flat stability of Llarull’s theorem in dimension three

By Brian Allen

46:21

published on November 14, 2023

Spacetime harmonic functions and applications

By Marcus Khuri

44:50

published on December 5, 2023

Ricci curvature, fundamental group and the Milnor conjecture (I)

By Aaron Naber

57:06

published on December 5, 2023

Ricci curvature, fundamental group and the Milnor conjecture (II)

By Daniele Semola

36:08

published on December 15, 2023

Spaces with Ricci curvature lower bounds

By Guofang Wei

01:00:32

published on December 15, 2023

Nonnegative Ricci curvature, nilpotency, and Hausdorff dimension

By Jiayin Pan

51:30

published on December 15, 2023

Stability of Llarull’s theorem in all dimensions

By Sven Hirsch

43:47

published on December 15, 2023

Some global effects of positive scalar curvature

By Yuguang Shi

46:32

published on February 2, 2024

Generic regularity in obstacle problems

By Alessio Figalli

48:55

published on February 2, 2024

Generic regularity for minimizing hypersurfaces in 9 and 10 dimensions

By Otis Chodosh

50:52

published on February 28, 2024

A stable version of Gromov’s angle-shrinking problem and its index theoretic applications (Part II)

By Jinming Wang

51:39

published on February 28, 2024

A stable version of Gromov’s angle-shrinking problem and its index theoretic applications (Part I)

By Zhizhang Xie

44:30

published on April 24, 2024

Positive mass theorem for asymptotically flat manifolds with isolated conical singularities

By Changliang Wang

48:20

published on April 24, 2024

Positive mass theorem and positive scalar curvature in the presence of a singularity

By Xianzhe Dai

48:32

published on May 9, 2024

Geometric variational methods to (not only) scalar curvature problems

By Chao Li

01:00:44

published on May 9, 2024

Another aspect of Gromov’s conjectures

By Tin-Yau Tsang

46:03

published on May 28, 2024

On spectra of Laplace and Dirac operators on noncompact manifolds

By Nadine Große

58:59

published on May 28, 2024

On the $L^p$ spectrum

By Nelia Charalambous

01:01:30

published on June 3, 2024

Waists measured via Urysohn width

By Alexey Balitskiy

38:42

published on June 3, 2024

Width, scalar curvature and macroscopic scalar curvature

By Yevgeny Liokumovich

58:19

published on June 18, 2024

Dimension-independent functional inequalities on sub-Riemannian manifolds

By Masha Gordina

47:30

published on June 18, 2024

Logarithmic Sobolev inequalities on homogeneous spaces

By Langbing Luo

01:21:15

published on October 4, 2024

Positive scalar curvature with point singularities

By Rudolf Zeidler

01:04:33

published on October 21, 2024

How hard is the theorem of Stolz?

By Fedor Manin

01:15:39

published on November 5, 2024

On the stability of spectra under coverings

By Werner Ballmann

01:03:08

published on December 4, 2024

Rigidity results for initial data sets satisfying the dominant energy condition

By Tsz-Kiu Aaron Chow

01:28:25

published on March 18, 2025

Macroscopic scalar curvature and volume

By Roman Sauer

01:12:26

published on March 31, 2025

How to define an inverse mean curvature flow coming out of crystals?

By Esther Cabezas-Rivas

01:03:18

published on April 14, 2025

Complete Riemannian 4-manifolds with uniformly positive scalar curvature metric

By Anubhav Mukherjee

54:22

published on April 27, 2025

Gradient estimates for scalar curvature

By Tobias Colding

49:07

published on June 1, 2025

On manifolds with almost non-negative Ricci curvature and integrally-positive kth-scalar curvature

By Andrea Mondino

01:09:59

published on November 7, 2025

Scalar curvature via Dirac eigenvalues

By Christian Bär

01:01:48

published on November 18, 2025

Small Scale Index Theory, Scalar Curvature, and Gromov’s Simplicial Norm

By Qiaochu Ma

56:07

published on November 18, 2025

3-Manifolds with positive scalar curvature and bounded geometry

By Yi Lai

55:53

published on November 27, 2025

Quaternion Kähler manifolds of non-negative sectional curvature

By Uwe Semmelmann

55:41

published on December 5, 2025

Application of Curvature Comparison Theorems in Minimal Surfaces

By Yujie Wu

Copyright Carmin.tv 2025

Give feedback