Complex torus, its good compactifications and the ring of conditions
Apparaît également dans la collection : Perspectives in real geometry / Perspectives en géométrie réelle
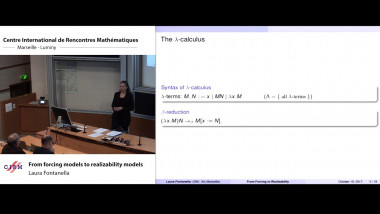
Let $X$ be an algebraic subvariety in $(\mathbb{C}^²)^n$. According to the good compactifification theorem there is a complete toric variety $M \supset (\mathbb{C}^²)^n$ such that the closure of $X$ in $M$ does not intersect orbits in $M$ of codimension bigger than dim$_\mathbb{C} X$. All proofs of this theorem I met in literature are rather involved. The ring of conditions of $(\mathbb{C}^²)^n$ was introduced by De Concini and Procesi in 1980-th. It is a version of intersection theory for algebraic cycles in $(\mathbb{C}^²)^n$. Its construction is based on the good compactification theorem. Recently two nice geometric descriptions of this ring were found. Tropical geometry provides the first description. The second one can be formulated in terms of volume function on the cone of convex polyhedra with integral vertices in $\mathbb{R}^n$. These descriptions are unified by the theory of toric varieties. I am going to discuss these descriptions of the ring of conditions and to present a new version of the good compactification theorem. This version is stronger that the usual one and its proof is elementary.












































































































![$k$-sum free sets in $[0,1]$](/media/cache/video_light/uploads/video/2015-09-10_de_Roton-video--19cf70874d3c5af7378c268cab865b06.jpg)