Paul Erdös et l’anatomie des nombres entiers
Avec le développement de la théorie des probabilités au début du XXe siècle, un nouveau champ d'investigation s'offre à l'arithmétique : étudier les nombres entiers non plus sous l'angle algébrique, comme par le passé, mais d'un point de vue statistique.
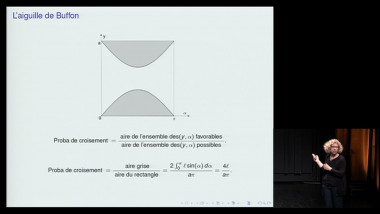
Que peut-on dire de « presque tout » nombre ? Et avec quelle précision ? En 1917 Hardy et Ramanujan montrent que le nombre des facteurs premiers d'un entier aléatoire peut être sommairement décrit à l'aide de sa seule taille. C'est la première naissance de la théorie probabiliste des nombres, dont le prodige hongrois Paul Erdös, né en 1913, est l'un des rares mathématiciens à saisir la portée dès le milieu des années 1930. En 1940, Erdös et Kac lient définitivement la théorie des nombres à celle des probabilités en montrant que le nombre des diviseurs premiers d'un entier suit statistiquement une loi de Gauss.
Ce résultat fondamental est le socle d'une branche florissante de l'arithmétique qui prend pour objet l'anatomie des entiers, autrement dit qui cherche à donner une idée statistique de leur structure multiplicative : comment les facteurs premiers sont-ils répartis ? Existe-t-il une loi standard pour passer d'un facteur au suivant ? Si oui, avec quelle précision peut-on la décrire ? etc. Nous nous proposons d'évoquer le personnage haut en couleurs de Paul Erdös et de donner quelques clefs pour appréhender ces découvertes d'une extraordinaire fécondité.