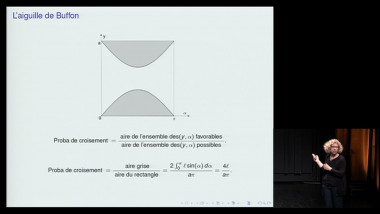
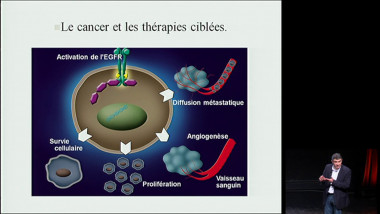
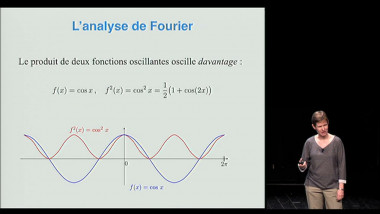
Le triangle de Pascal et ses propriétés
On sait bien que Blaise Pascal fut un mathématicien et un physicien génial avant de se consacrer à la théologie et la philosophie. Parmi ses travaux mathématiques figure l'important Traité du triangle arithmétique de 1654. Même si le tableau de nombres entiers qui y est défini avait déjà été étudié plusieurs siècles auparavant par Yang Hui et Omar Khayyam, c'est bien sous le nom de «triangle de Pascal» qu'il est connu jusqu'à nos jours.
Les nombres apparaissant dans le triangle de Pascal (appelés coefficients binomiaux) sont utiles dans de nombreuses situations, depuis les identités remarquables de l'algèbre jusqu'à des problèmes combinatoires complexes, en passant par le calcul des chances de gagner au Loto.
L'arithmétique (ou théorie des nombres) est la branche des mathématiques qui s'intéresse aux propriétés des nombres entiers, notamment aux questions de divisibilité et aux nombres premiers (ceux qui ne sont divisibles que par 1 et eux-mêmes). Les concepts mathématiques qui ont été inventés, depuis les Grecs, et plus particulièrement au XIXème et au XXème siècle par les mathématiciens pour percer à jour les mystères des nombres premiers est particulièrement riche. Parmi ceux-ci, la fonction zeta de Riemann joue un rôle tout à fait central.
Les coefficients binomiaux ont des propriétés arithmétiques dont certaines sont bien connues, mais d'autres n'ont été découvertes que récemment, apportant un éclairage nouveau aux recherches sur les nombres premiers.