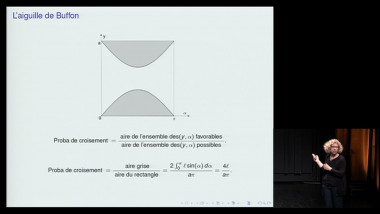
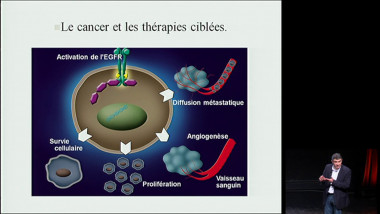
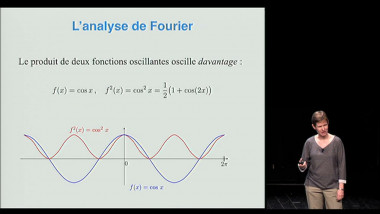
Espaces courbes de Gauss à Perelman, en passant par Einstein
Carl Friedrich Gauss est un des plus importants mathématiciens à la charnière des XVIIIème et XIXème siècles. Il a apporté des avancées majeures dans des domaines très divers des mathématiques. Il s'est particulièrement intéressé à la géométrie des surfaces, se demandant notamment comment on peut percevoir qu'une surface est "courbée" sans l'observer de l'extérieur – par exemple comment mesurer que la Terre n'est pas exactement sphérique.
Le document de Carl Friedrich Gauss qui contient l'acte de naissance de la notion de courbure intrinsèque, qui répond à cette question, par opposition à celle dite extrinsèque qui fait intervenir un espace plus grand dans lequel l'espace étudié serait plongé est les "Disquisitiones generales circa superficies curvas" publiées en 1828. La notion d'espace courbe s'est avérée centrale dans les développements ultérieurs de la géométrie jusqu'à nos jours, d'abord dans le cadre de la grandiose généralisation de la géométrie due à Bernhard Riemann puis dans celui de la relativité générale d'Albert Einstein et tout récemment pour la solution de la conjecture de Poincaré par Grisha Perelman. Le concept de courbure s'est révélé pertinent dans plusieurs champs scientifiques autres que les mathématiques comme la physique.