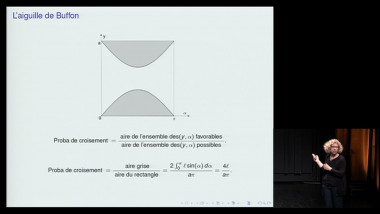
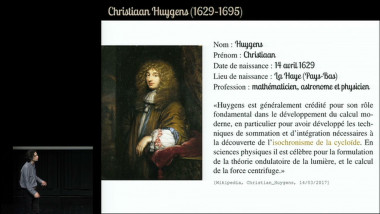
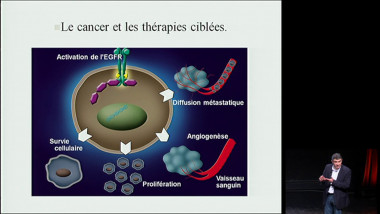
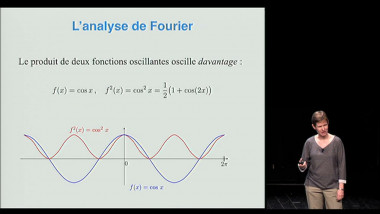
Le génie interrompu d’Alan Turing
Les ponts, les avions, et les bicyclettes ont été construits bien avant qu’une théorie scientifique soit à même d’expliquer leur fonctionnement. L’ordinateur fait figure d’exception, étant en effet une des rares technologies dont la théorie a précédé la réalisation. En 1936, Alan Turing écrit le texte fondateur de l’informatique, qui est le sujet de cette conférence. Il faudra attendre une dizaine d’années avant que le premier ordinateur ne voie le jour. Formé aux mathématiques et à la physique à l’université de Cambridge, Turing se distingue rapidement par l’originalité et l’éclectisme de sa pensée. On lui doit des contributions scientifiques majeures dans des disciplinées aussi variées que la théorie des nombres, la logique, la biologie, la cryptographie, les statistiques, et l’intelligence artificielle.
Alan Turing aura connu une vie courte et mouvementée, refusant de se plier aux normes rigides d’une société dont l’intolérance le conduira au suicide à l’âge de 41 ans. De son œuvre scientifique, l’histoire retiendra deux grands chapitres. D’une part, la conception de l’ordinateur moderne, une découverte à l’origine de la plus grande révolution technologique que le monde ait connu depuis le XIXème siecle ; d’autre part, le déchiffrement du code secret nazi. A cet égard, Churchill n’hésitera pas à designer Turing comme l’individu ayant contribué le plus à la victoire alliée pendant la deuxième guerre mondiale.
Cette conférence s’efforcera d’expliquer l’innovation radicale du papier de Turing de 1936. Alors que l’approche dominante de l’époque était d’amarrer la notion de calcul au formalisme de la logique, c’est au mathématicien Alan Turing de proposer que la perspective à adopter n’est pas celle du logicien mais de l’ingénieur : selon lui, le calcul est avant tout affaire de «machine». Les conséquences ne se font pas attendre. Non seulement l’approche «mécanique» de Turing permet d’étendre et de simplifier les résultats célèbres de Gödel sur l’incomplétude des systèmes formels mais, surtout, elle ouvre la voie vers les ordinateurs électroniques et l’algorithmique qui les gouverne.