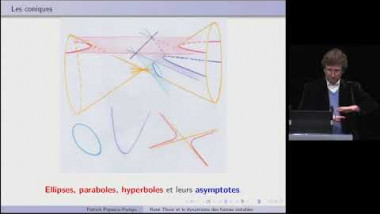
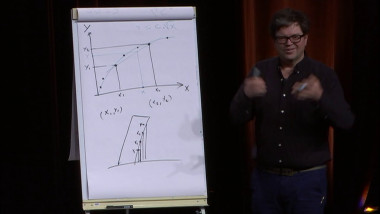
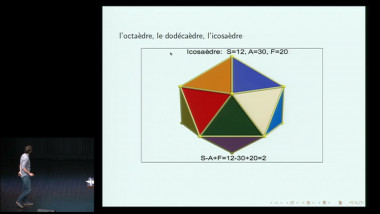
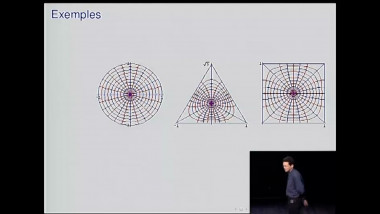
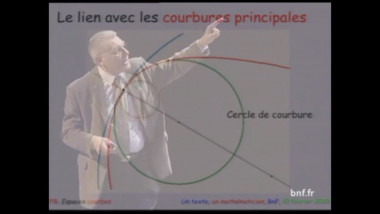
Le symbolisme mathématique : des figures aux nombres et à leurs transfigurations
Joseph-Louis Lagrange est un mathématicien italien né à Turin le 25 janvier 1736 et mort à Paris en 1813. Dès l’age de 18 ans il se fait connaître dans les milieux mathématiques, notamment par Euler, ce qui lui vaut son élection à l’académie de Berlin en 1756. Sa carrière commence dans sa ville natale de Turin, puis à Berlin en 1766, et enfin à Paris à partir de 1787. Il y sera membre de l’Académie royale des sciences, professeur à la toute jeune Ecole normale, puis à l’Ecole polytechnique, connaissant également une reconnaissance éminente puisqu’il fut nommé sénateur et comte d’empire par Napoléon. Il est enterré au Panthéon. La Mécanique est la science du mouvement des objets : chute des corps, mouvement des planètes, écoulement des liquides etc. On sait bien combien sont riches les relations entre Mécanique et mathématiques. Mais la publication par Lagrange de sa Mécanique analytique en 1788 représente un tournant dans l'histoire de cette science : ce qu’on appelle le « formalisme lagrangien » est aujourd’hui encore un des aspects essentiels de la Mécanique. Un des éléments frappants est son insistance à tout réduire à une forme algébrique, sans aucun raisonnement géométrique, ni figure ; ainsi dans son avertissement, il écrit : « Les méthodes que j'y expose ne demandent ni constructions, ni raisonnements géométriques ou mécaniques, mais seulement des opérations algébriques, assujetties à une marche régulière et uniforme. » Il s'agit bien sûr d'une continuation de la géométrie des coordonnées de Descartes, mais avec une vigueur inconnue jusque-là. Cependant, l'histoire de l’algébrisation des mathématiques ne s'est pas terminée là, et tout le dix-neuvième siècle a été à la recherche d'un formalisme algébrique aussi fidèle que possible à la réalité géométrique (quaternions , vecteurs , invariants et matrices, calcul de Grassmann). La fin du vingtième siècle voit un nouveau développement : un calcul direct sur des figures (graphes, tableaux, diagrammes , arbres , ...). Ce sont là quelques étapes dans la recherche d'un symbolisme mathématique toujours plus adapté.