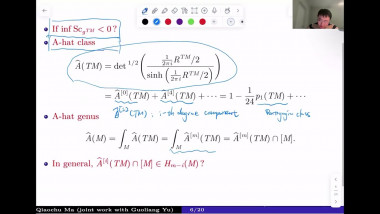
Scalar curvature via Dirac eigenvalues
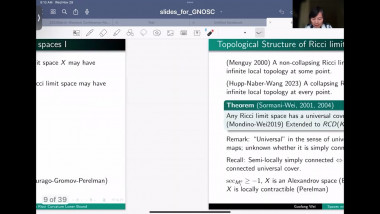
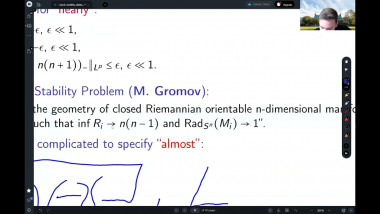
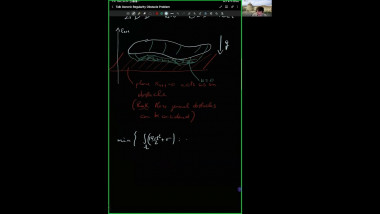
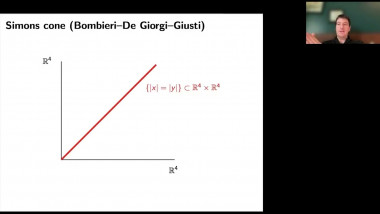
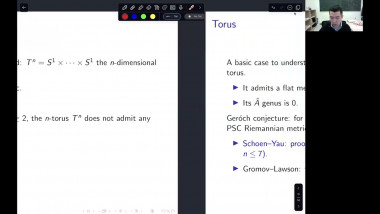
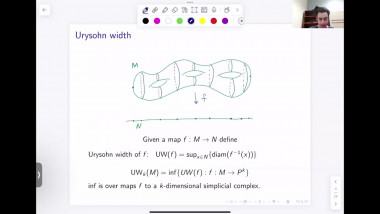
Scalar curvature encodA relation between the hyperspherical radius and Dirac eigenvalues will be used to give simple proofs of some classical rigidity results for scalar curvature. This includes Llarull's theorem, the Geroch conjecture and a recent inequality for fill-ins with nonnegtive scalar curvature. A new relation between the hyperspherical radius and the Yamabe invariant will be established. After that, the condition in Llarull's theorem that the comparison map has nonzero degree will be discussed.