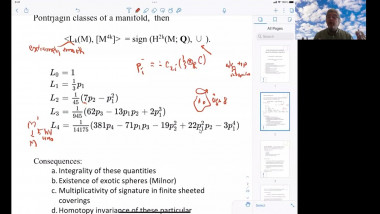
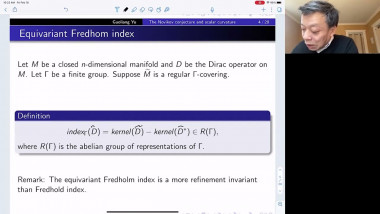
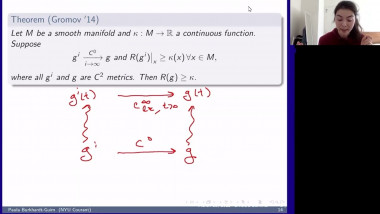
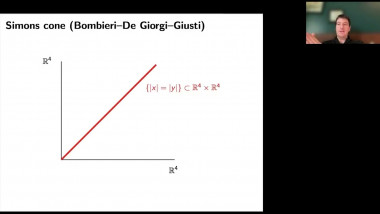
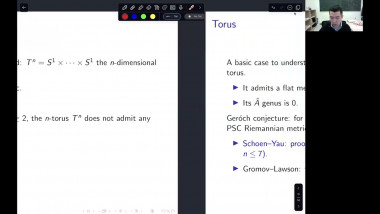
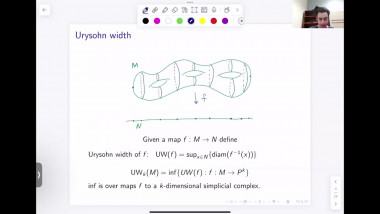
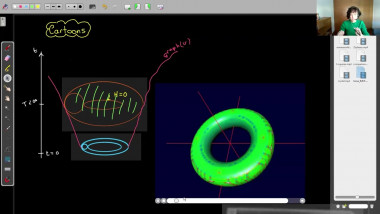
Index theory and applications to scalar curvature
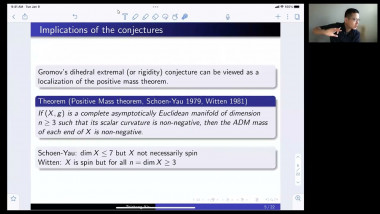
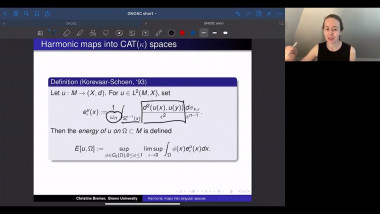
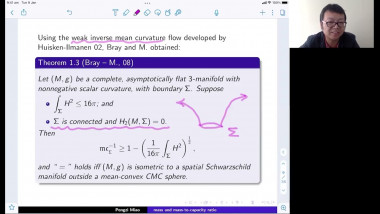
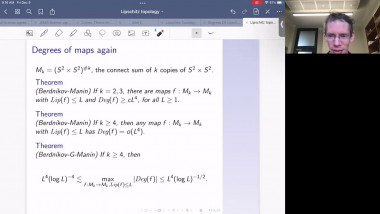
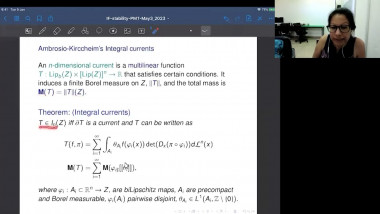
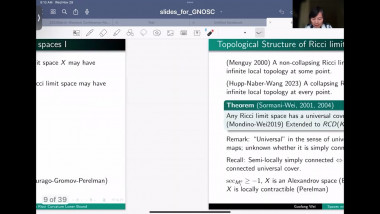
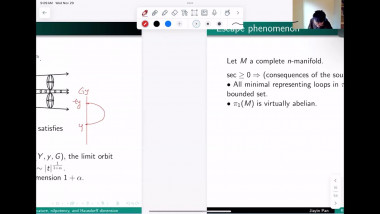
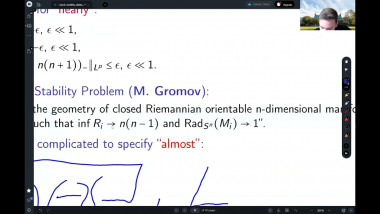
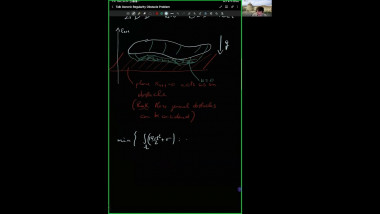
In the first part of the talk I will discuss two index theorems for compact manifolds with boundary. The first one computes the index of a specific boundary value problem for a Dirac operator in terms of the Euler number of the manifold. The second one relates the index of a boundary value problem to the index of an operator on the boundary. Both theorems have applications to scalar curvature geometry. I will describe such applications for the second theorem. The first index theorem will come up in the second talk by Yipeng Wang. This is based on joint work with Simon Brendle, Bernhard Hanke, and Yipeng Wang