Spaces with Ricci curvature lower bounds
De Guofang Wei
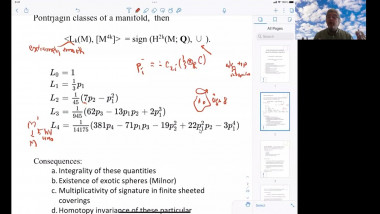
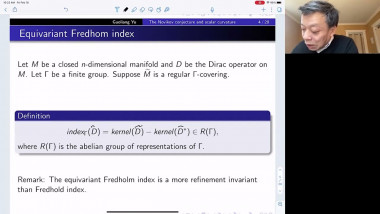
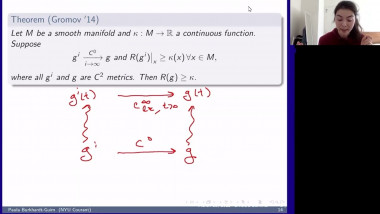
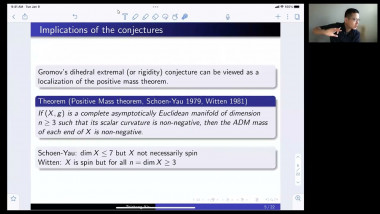
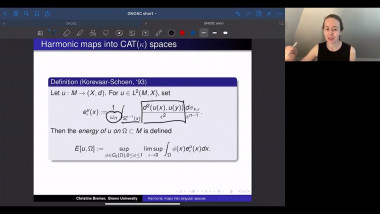
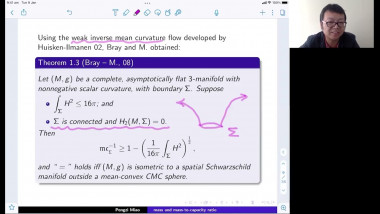
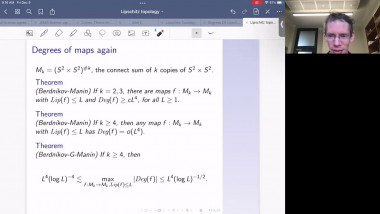
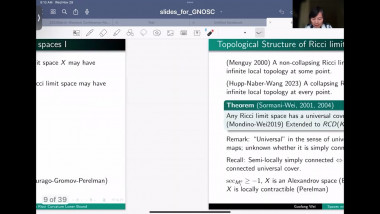
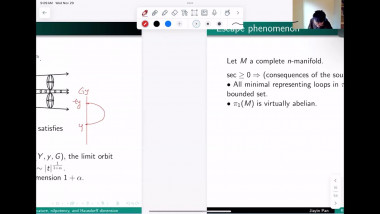
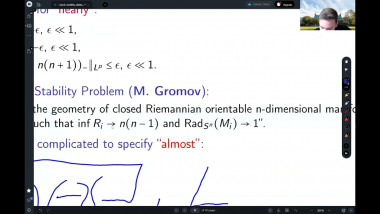
We will survey some recent results on the geometry and topology of spaces with nonnegative Ricci curvature showing dramatic new features for Ricci curvature lower bound. We will focus on joint work with J. Pan. First, the construction of Ricci limit spaces for which the Hausdorff dimension of the singular set is bigger than the Hausdorff dimension of the regular set, answering a question of Cheeger-Colding in 2000 in negative. This leads to, joint with X. Dai, S. Honda, J. Pan, two surprising types of Weyl’s laws which are fractal-like for some compact Ricci limit spaces. Then I will present, also joint with J. Pan, examples of manifolds with nonnegative Ricci curvature but nonproper Busemann function which were open since the 70's.