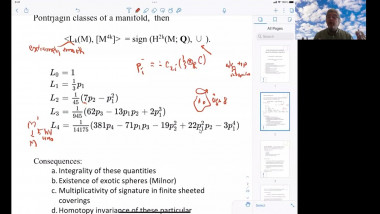
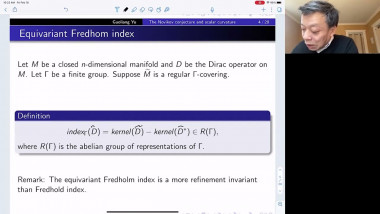
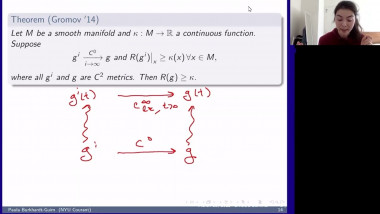
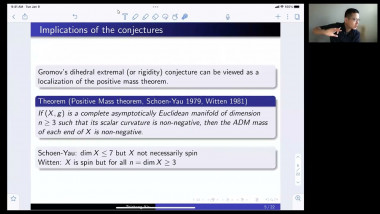
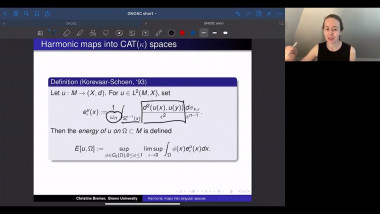
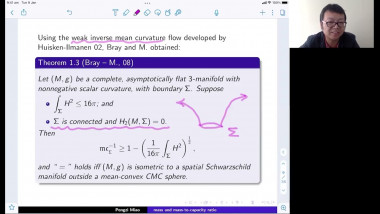
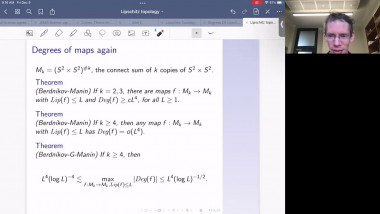
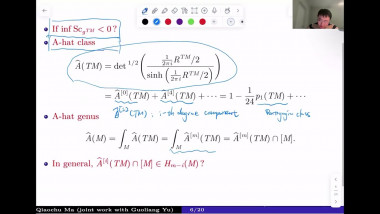
Positive scalar curvature with point singularities
I will explain a certain topological construction of positive scalar curvature metrics with uniformly Euclidean ($L^\infty$) point singularities. This provides counterexamples to a conjecture of Schoen. It also shows that there are metrics with uniformly Euclidean point singularities which cannot be smoothed via a geometric flow while simultaneously preserving non-negativity of the scalar curvature. Based on recent joint work with Simone Cecchini and Georg Frenck (arXiv:2407.20163).
