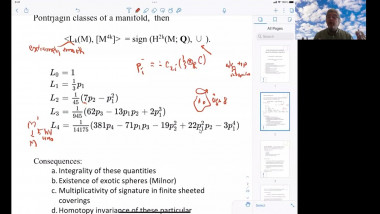
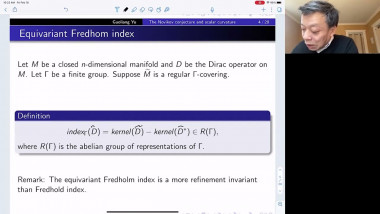
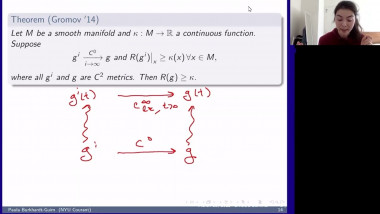
Positive mass theorem for asymptotically flat manifolds with isolated conical singularities
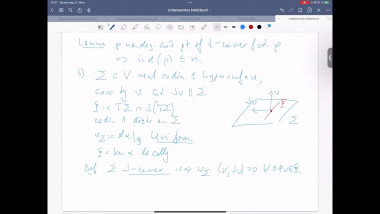
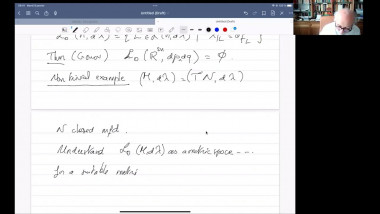
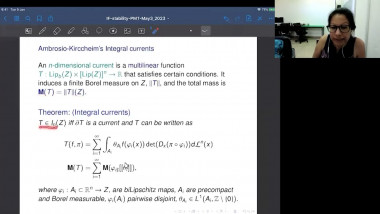
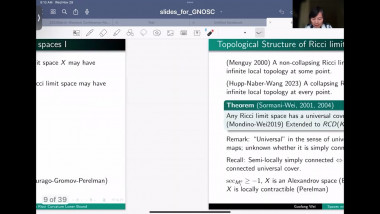
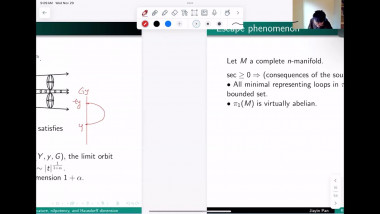
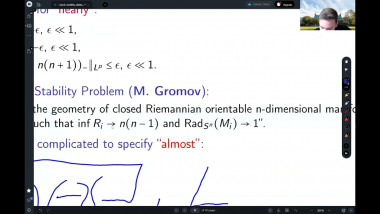
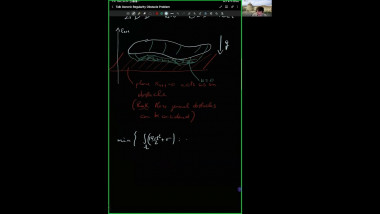
In this talk, I will mainly report recent joint works with Xianzhe Dai and Yukai Sun on positive mass theorem (PMT) for asymptotically flat (AF) manifolds with isolated conical singularities. In spin setting, we extend Witten’s argument by solving Dirac operator on AF manifolds with isolated conical singularities. In non-spin setting, we apply the conformal blow up technique and Hirsch-Miao’s PMT on AF manifolds with boundary. Here we solve Laplace equation on conically singular AF manifolds. For proving the rigidity result, we also need a partial asymptotical expansion for solutions. Moreover, with the help of these analysis on conically singular manifolds, by applying conformal blow up technique and Chodosh-Li’s and Wang-Zhang’s generalized Geroch type results on complete manifold, we prove a Geroch type result for isolated conical singularity.
