Quaternion Kähler manifolds of non-negative sectional curvature
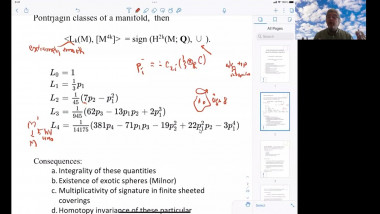
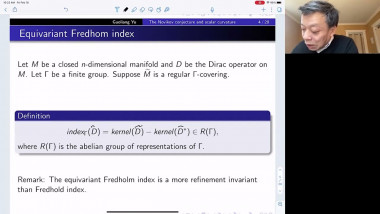
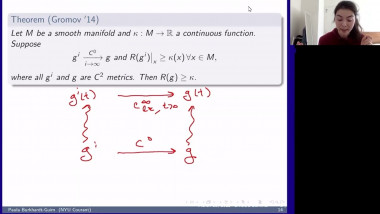
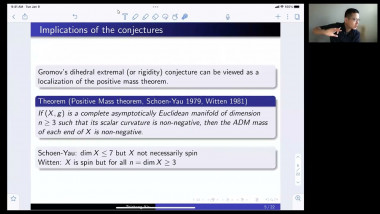
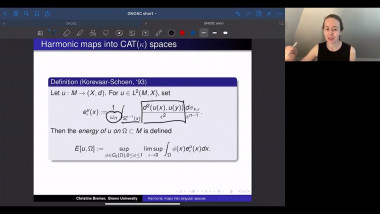
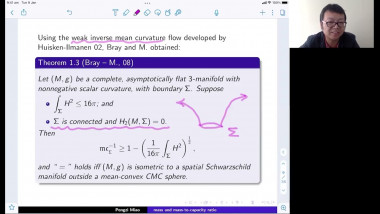
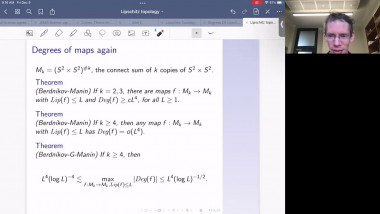
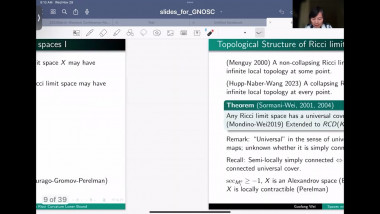
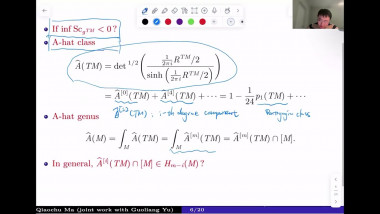
Quaternion Kähler manifolds, i.e. Riemannian manifolds with holonomy contained in Sp(m)Sp(1), are Einstein. In the case of positive scalar curvature, there is a longstanding conjecture by LeBrun and Salamon stating that all such manifolds should be symmetric. So far, the conjecture has been confirmed only up to dimension 12. In the first part of my talk I will give an introduction to the geometry of quaternion Kähler manifolds of positive scalar curvature. In the second part I will make a few remarks on the proof of the conjecture under the additional assumption of non-negative sectional curvature. This extends earlier work by Berger, who proved that quaternion Kähler manifolds of positive sectional curvature are isometric to the quaternionic projective space. My talk is based on a joint article with Simon Brendle and on earlier work by Simon Brendle.