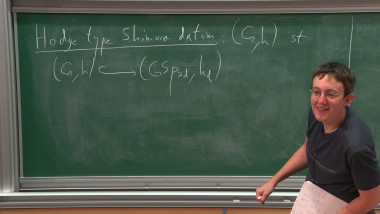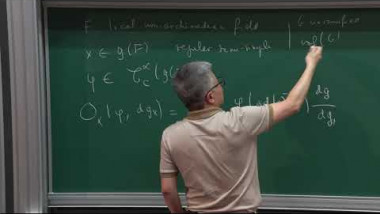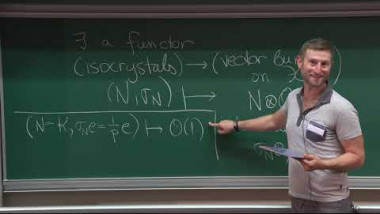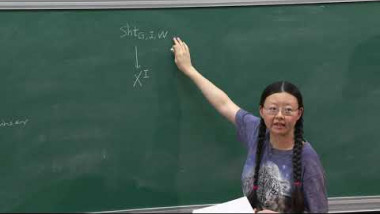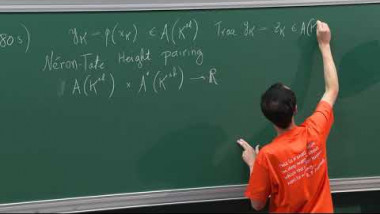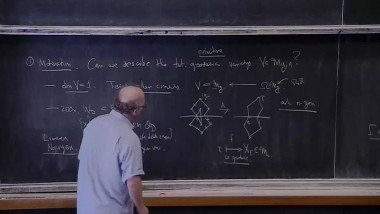Summer School on the Langlands Program

Collection Summer School on the Langlands Program

Organizer(s) Pierre-Henri Chaudouard, Wee Teck Gan, Tasho Kaletha, Yiannis Sakellaridis

Date(s) 11/07/2022 - 29/07/2022

linked URL https://indico.math.cnrs.fr/event/6909/

00:00:00 / 00:00:00

49 58

Shimura Varieties and Modularity (3/3)

By Ana Caraiani, Sug Woo Shin

We discuss vanishing theorems for the cohomology of Shimura varieties with torsion coefficients, under a genericity condition at an auxiliary prime. We describe two complementary approaches to these results, due to Caraiani-Scholze and Koshikawa, both of which rely on the geometry of the Hodge-Tate period morphism for the corresponding Shimura varieties. Finally, we explain how these vanishing results can be applied to local-global compatibility questions for the Galois representations constructed in the first lecture.

Information about the video

Date of recording 27/07/2022
Date of publication 27/07/2022
Institution IHES
Language English
Audience Researchers, Graduate Students
Format MP4

Domain(s)

Last related questions on MathOverflow

You have to connect your Carmin.tv account with mathoverflow to add question

Ask a question on MathOverflow

All the collection videos

01:20:52

published on July 12, 2022

The Local Langlands Conjecture (1/3)

By Olivier Taïbi

01:16:42

published on July 12, 2022

Some Perspectives on Eisenstein Series (1/2)

By Erez Lapid

01:04:43

published on July 12, 2022

The Local Langlands Conjecture (2/3)

By Olivier Taïbi

01:07:41

published on July 12, 2022

Shimura Varieties (1/3)

By Sophie Morel

01:39:10

published on July 12, 2022

Introduction to the (Relative) Trace Formula (1/2)

By Pierre-Henri Chaudouard

01:00:49

published on July 13, 2022

Some Perspectives on Eisenstein Series (2/2)

By Erez Lapid

01:07:28

published on July 12, 2022

Shimura Varieties (2/3)

By Sophie Morel

01:00:49

published on July 13, 2022

The Local Langlands Conjecture (3/3)

By Olivier Taïbi

01:17:38

published on July 13, 2022

Introduction to the (Relative) Trace Formula (2/2)

By Pierre-Henri Chaudouard

01:23:44

published on July 13, 2022

Arthur's Conjectures and the Orbit Method for Real Reductive Groups

By Lucas Mason-Brown

01:03:33

published on July 13, 2022

Introduction to Shtukas and their Moduli (1/3)

By Zhiwei Yun

01:04:05

published on July 13, 2022

Shimura Varieties (3/3)

By Sophie Morel

01:24:11

published on July 14, 2022

The Relative Langlands Program (1/3)

By Raphaël Beuzart Plessis

01:22:24

published on July 14, 2022

Coherent Sheaves on the Stack of Langlands Parameters (1/3)

By Xinwen Zhu

59:23

published on July 14, 2022

Introduction to Shtukas and their Moduli (2/3)

By Zhiwei Yun

01:04:55

published on July 14, 2022

Introduction to Shtukas and their Moduli (3/3)

By Zhiwei Yun

01:25:38

published on July 15, 2022

The Relative Langlands Program (2/3)

By Raphaël Beuzart Plessis

01:19:33

published on July 15, 2022

Coherent Sheaves on the Stack of Langlands Parameters (2/3)

By Xinwen Zhu

01:04:18

published on July 16, 2022

Coherent Sheaves on the Stack of Langlands Parameters (3/3)

By Xinwen Zhu

01:03:17

published on July 16, 2022

The Relative Langlands Program (3/3)

By Raphaël Beuzart Plessis

01:26:25

published on July 18, 2022

A Brief Introduction to the Trace Formula and its Stabilization (1/2)

By Tasho Kaletha

01:18:05

published on July 18, 2022

Local Shtukas and the Langlands Program (1/2)

By Jared Weinstein

01:02:00

published on July 18, 2022

Orbital integrals, moduli spaces and invariant theory (1/3)

By Bao Chau Ngo

53:16

published on July 18, 2022

Orbital integrals, moduli spaces and invariant theory (2/3)

By Bao Chau Ngo

01:24:28

published on July 19, 2022

Local Shtukas and the Langlands Program (2/2)

By Jared Weinstein

01:29:54

published on July 19, 2022

A Brief Introduction to the Trace Formula and its Stabilization (2/2)

By Tasho Kaletha

01:06:01

published on July 19, 2022

Cohomology Sheaves of Stacks of Shtukas (1/2)

By Cong Xue

01:08:20

published on July 20, 2022

Cohomology Sheaves of Stacks of Shtukas (2/2)

By Cong Xue

01:31:40

published on July 20, 2022

An Introduction to the Categorical p-adic Langlands Program (1/4)

By Matthew Emerton , Toby Gee , Eugen Hellmann

01:25:38

published on July 20, 2022

Orbital integrals, moduli spaces and invariant theory (3/3)

By Bao Chau Ngo

01:02:30

published on July 21, 2022

What does geometric Langlands mean to a number theorist? (1/2)

By Sam Raskin

01:30:43

published on July 21, 2022

What does geometric Langlands mean to a number theorist? (2/2)

By Sam Raskin

01:26:55

published on July 21, 2022

The Langlands Program and the Moduli of Bundles on the Curve (1/3)

By Peter Scholze , Laurent Fargues

01:24:22

published on July 21, 2022

Explicit Constructions of Automorphic Forms (1/2)

By Wee Teck Gan

01:05:10

published on July 21, 2022

An Introduction to the Categorical p-adic Langlands Program (2/4)

By Matthew Emerton , Toby Gee , Eugen Hellmann

01:07:10

published on July 22, 2022

An Introduction to the Categorical p-adic Langlands Program (3/4)

By Matthew Emerton , Toby Gee , Eugen Hellmann

01:24:15

published on July 22, 2022

On Moduli Spaces of Local Langlands Parameters (1/2)

By Jean-François Dat

01:23:03

published on July 22, 2022

Explicit Constructions of Automorphic Forms (2/2)

By Wee Teck Gan

01:03:25

published on July 24, 2022

Supercuspidal Representations: Construction, Classification, and Characters (1/2)

By Jessica Fintzen

01:07:10

published on July 24, 2022

The Langlands Program and the Moduli of Bundles on the Curve (2/3)

By Peter Scholze , Laurent Fargues

01:28:15

published on July 25, 2022

An Introduction to the Categorical p-adic Langlands Program (4/4)

By Matthew Emerton , Toby Gee , Eugen Hellmann

01:22:23

published on July 25, 2022

Supercuspidal Representations: Construction, Classification, and Characters (2/2)

By Jessica Fintzen

01:01:47

published on July 26, 2022

Branching laws: homological aspects

By Dipendra Prasad

01:07:27

published on July 26, 2022

On Moduli Spaces of Local Langlands Parameters (2/2)

By Jean-François Dat

01:20:27

published on July 27, 2022

The Langlands Program and the Moduli of Bundles on the Curve (3/3)

By Peter Scholze , Laurent Fargues

01:27:06

published on July 26, 2022

Shimura Varieties and Modularity (1/3)

By Ana Caraiani , Sug Woo Shin

01:04:30

published on July 27, 2022

Shimura Varieties and Modularity (2/3)

By Ana Caraiani , Sug Woo Shin

01:02:30

published on July 27, 2022

Geometric and Arithmetic Theta Correspondences (1/2)

By Chao Li

01:27:05

published on July 27, 2022

Shimura Varieties and Modularity (3/3)

By Ana Caraiani , Sug Woo Shin

01:17:59

published on July 28, 2022

Geometric and Arithmetic Theta Correspondences (2/2)

By Chao Li

01:26:19

published on July 28, 2022

High-dimensional Gross–Zagier Formula (1/2)

By Wei Zhang

01:27:27

published on July 28, 2022

Between Coherent and Constructible Local Langlands Correspondences

By David Ben-Zvi

01:08:29

published on July 29, 2022

Derived Aspects of the Langlands Program (1/3)

By Michael Harris , Tony Feng

01:04:08

published on July 29, 2022

Local and Global Questions “Beyond Endoscopy” (1/2)

By Yiannis Sakellaridis

01:20:48

published on July 29, 2022

Derived Aspects of the Langlands Program (2/3)

By Michael Harris , Tony Feng

01:27:18

published on July 29, 2022

High-dimensional Gross–Zagier Formula (2/2)

By Wei Zhang

01:03:24

published on July 29, 2022

Local and Global Questions “Beyond Endoscopy” (2/2)

By Yiannis Sakellaridis

01:04:31

published on July 29, 2022

Derived Aspects of the Langlands Program (3/3)

By Michael Harris , Tony Feng

Copyright Carmin.tv 2024

Give feedback