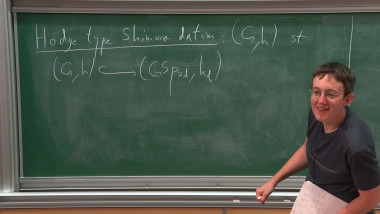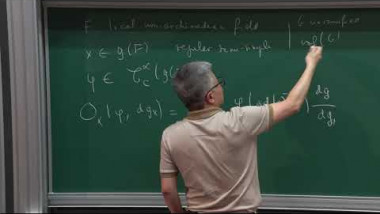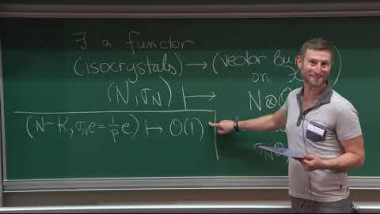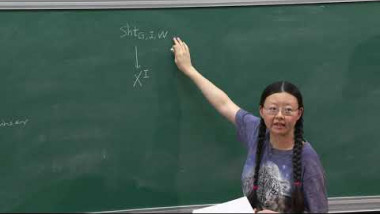A Brief Introduction to the Trace Formula and its Stabilization (1/2)
We will discuss the derivation of the stable Arthur-Selberg trace formula. In the first lecture we will focus on anisotropic reductive groups, for which the trace formula can be derived easily. We will then discuss the stabilization of this trace formula, which is unconditional on the geometric side, and relies on the Arthur conjectures on the spectral side. In the second lecture we will sketch the case of an arbitrary reductive group, which causes many analytic difficulties. We will briefly describe the various stops on the road to the stable trace formula, including the coarse and fine expansions of the non-invariant trace formula, as well the invariant trace formula. Examples will be given for the group SL_2. Towards the end, we will discuss the application of the stable trace formula to the classification of representations of classical groups.