Carmin.tv

Mathématiques
et Interactions

Merci de nous donner votre avis pour que nous puissions améliorer votre expérience !
Balzan Lectures
10 videos

Balzan Lectures

Jean Morlet Chair - 2024 - Sem 2 - Collins - Demni
1 videos

Jean Morlet Chair - 2024 - Sem 2 - Collins - Demni

Jean Morlet Chair - Research school: Random quantum channels: entanglement and entropies / Chaire Jean Morlet - Ecole: Canaux quantiques aléatoires: Intrication et entropies
5 videos

Jean Morlet Chair - Research school: Random quantum channels: entanglement and entropies / Chaire Jean Morlet - Ecole: Canaux quantiques aléatoires: Intrication et entropies

Research School - Jean Morlet Chair - Frontiers in Interacting Particle Systems, Aggregation-Diffusion Equations & Collective Behavior / Ecole - Chaire Jean Morlet - Frontières dans les équations de systèmes de particules en interaction. Equations d'agrégation-diffusion et comportement collectif
7 videos

Research School - Jean Morlet Chair - Frontiers in Interacting Particle Systems, Aggregation-Diffusion Equations & Collective Behavior / Ecole - Chaire Jean Morlet - Frontières dans les équations de systèmes de particules en interaction. Equations d'agrégation-diffusion et comportement collectif

Toutes les collections
CIMPA
CIRM
IHES
IHP
LMR
SMF
Tous les instituts
Combinatorics and Arithmetic for Physics: special days 2023

Collection Combinatorics and Arithmetic for Physics: special days 2023

Organisateur(s) Gérard H. E. DUCHAMP, Maxim KONTSEVICH, Gleb KOSHEVOY, Sergei NECHAEV and Karol A. PENSON
Date(s) 15/11/2023 - 17/11/2023
URL associée https://www-lipn.univ-paris13.fr/~duchamp/Conferences/CAP10_2023.html
00:00:00 / 00:00:00
22 27

Crystal operators on Cluster Algebras

De Volker Genz

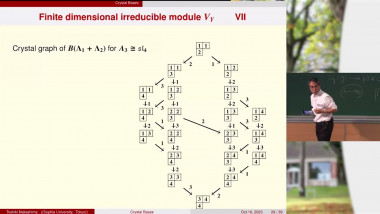
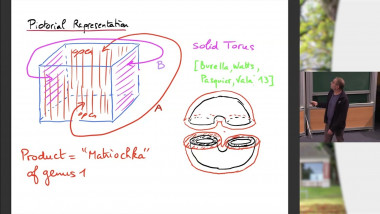
Crystal operators on canonical bases as introduced by Kashiwara/Lusztig provide in particular a toolbox to compute within the category of finite dimensional representations of finite dimensional simple Lie algebras. Motivated by this we previously introduced certain operators on the lattice of tropical points of mirror dual A- and X-cluster spaces. In this talk we give an update. In particular, the crystal structure gives rise to a binary operation on the canonical basis due to Gross-Hacking-Keel-Kontsevich. We expect this to have a wider range of applications in the theory of cluster algebras and in physics.

Informations sur la vidéo

  • Date de captation 17/11/2023
  • Date de publication 22/11/2023
  • Institut IHES
  • Langue Anglais
  • Audience Chercheurs
  • Format MP4

Domaine(s)

Dernières questions liées sur MathOverflow

Pour poser une question, votre compte Carmin.tv doit être connecté à mathoverflow

Poser une question sur MathOverflow




Inscrivez-vous

  • Mettez des vidéos en favori
  • Ajoutez des vidéos à regarder plus tard &
    conservez votre historique de consultation
  • Commentez avec la communauté
    scientifique
  • Recevez des notifications de mise à jour
    de vos sujets favoris
Copyright Carmin.tv 2024
En poursuivant votre navigation sur ce site, vous acceptez l'utilisation de cookies pour améliorer votre expérience. En savoir plus sur notre politique de confidentialité.
Accepter
Donner son avis