Carmin.tv

Mathématiques
et Interactions

Merci de nous donner votre avis pour que nous puissions améliorer votre expérience !
Not Only Scalar Curvature Seminar
60 videos

Not Only Scalar Curvature Seminar

Albert Schwarz : Quantum Mechanics and Quantum Field Theory from Algebraic and Geometric Viewpoints
2 videos

Albert Schwarz : Quantum Mechanics and Quantum Field Theory from Algebraic and Geometric Viewpoints

Clément Delcamp : Topological Symmetry and Duality in Quantum Lattice Models
4 videos

Clément Delcamp : Topological Symmetry and Duality in Quantum Lattice Models

Aggregation-Diffusion Equations & Collective Behavior: Analysis, Numerics and Applications / Conférence Chaire Jean Morlet: Equations d'agrégation-diffusion et comportement collectif: Analyse, schémas numériques et applications
5 videos

Aggregation-Diffusion Equations & Collective Behavior: Analysis, Numerics and Applications / Conférence Chaire Jean Morlet: Equations d'agrégation-diffusion et comportement collectif: Analyse, schémas numériques et applications

Toutes les collections
CIMPA
CIRM
IHES
IHP
LMR
SMF
Tous les instituts
Combinatorics and Arithmetic for Physics: special days 2023

Collection Combinatorics and Arithmetic for Physics: special days 2023

Organisateur(s) Gérard H. E. DUCHAMP, Maxim KONTSEVICH, Gleb KOSHEVOY, Sergei NECHAEV and Karol A. PENSON
Date(s) 15/11/2023 - 17/11/2023
URL associée https://www-lipn.univ-paris13.fr/~duchamp/Conferences/CAP10_2023.html
00:00:00 / 00:00:00
13 27

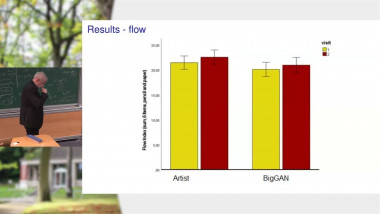
What does perturbative field theory teaches us on the statistical properties of Monge-Kantorovich Optimal Transportation in dimension 2?

De Andrea Sportiello

We all know that Feynman diagrams and integrals describe quantities in Particle Physics, and, sometimes, in Statistical Mechanics. We also know that, in these circumstances, we have to learn how to ”deal with infinities”, and regularise certain divergences. It may appear more suprising that the same ideas apply to this famous old problem in Functional Analysis, and also the same pathologies do arise. But at least, in this case, we see more clearly where do they come from. The precise content of the talk is still to be determined, but the message shall be twofold: on one side, we get results on the Optimal Transportation Problem in itself; on the other side, we learn a lesson on why a more naive approach does fail, while a more accurate approach allows to cure the apparent divergences, which could be of general interest.

Informations sur la vidéo

  • Date de captation 16/11/2023
  • Date de publication 22/11/2023
  • Institut IHES
  • Langue Anglais
  • Audience Chercheurs
  • Format MP4

Dernières questions liées sur MathOverflow

Pour poser une question, votre compte Carmin.tv doit être connecté à mathoverflow

Poser une question sur MathOverflow




Inscrivez-vous

  • Mettez des vidéos en favori
  • Ajoutez des vidéos à regarder plus tard &
    conservez votre historique de consultation
  • Commentez avec la communauté
    scientifique
  • Recevez des notifications de mise à jour
    de vos sujets favoris
Copyright Carmin.tv 2024
En poursuivant votre navigation sur ce site, vous acceptez l'utilisation de cookies pour améliorer votre expérience. En savoir plus sur notre politique de confidentialité.
Accepter
Donner son avis