Carmin.tv

Mathématiques
et Interactions

Merci de nous donner votre avis pour que nous puissions améliorer votre expérience !
Numerical Linear Algebra / Algèbre Linéaire Numérique
4 videos

Numerical Linear Algebra / Algèbre Linéaire Numérique

School/Workshop: Energy, mathematics, and theoretical challenges
21 videos

School/Workshop: Energy, mathematics, and theoretical challenges

Not Only Scalar Curvature Seminar
67 videos

Not Only Scalar Curvature Seminar

An introduction to dynamics on surfaces and random walks / Géométrie et Dynamiques sur les surfaces
11 videos

An introduction to dynamics on surfaces and random walks / Géométrie et Dynamiques sur les surfaces

Toutes les collections
CIMPA
CIRM
IHES
IHP
LMR
SMF
Tous les instituts
Combinatorics and Arithmetic for Physics: special days 2023

Collection Combinatorics and Arithmetic for Physics: special days 2023

Organisateur(s) Gérard H. E. DUCHAMP, Maxim KONTSEVICH, Gleb KOSHEVOY, Sergei NECHAEV and Karol A. PENSON
Date(s) 15/11/2023 - 17/11/2023
URL associée https://www-lipn.univ-paris13.fr/~duchamp/Conferences/CAP10_2023.html
00:00:00 / 00:00:00
18 27

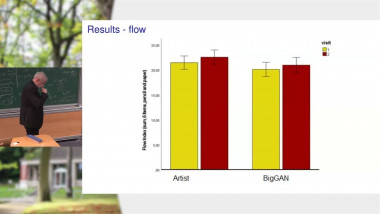
The Redei–Berge symmetric function of a directed graph

De Darij Grinberg

In 1934, Laszlo Redei observed a peculiar property of tournaments (directed graphs that have an arc between every pair of distinct vertices): Each tournament has an odd number of Hamiltonian paths. In 1996, Chow introduced the “path-cycle symmetric function” of a directed graph, a symmetric function in two sets of arguments, which was later used in rook theory. We study Chow’s symmetric function in the case when the y-variables are 0. In this case, we give new nontrivial expansions of the function in terms of the power-sum basis; in particular, we find that it is p-positive as long as the directed graph has no 2-cycles. We use our expansions to reprove Redei’s theorem and refine it to a mod-4 congruence. Joint work with with Richard P. Stanley.

Informations sur la vidéo

  • Date de publication 22/11/2023
  • Institut IHES
  • Audience Chercheurs
  • Format MP4

Domaine(s)

Codes MSC

Document(s)

Dernières questions liées sur MathOverflow

Pour poser une question, votre compte Carmin.tv doit être connecté à mathoverflow

Poser une question sur MathOverflow




Inscrivez-vous

  • Mettez des vidéos en favori
  • Ajoutez des vidéos à regarder plus tard &
    conservez votre historique de consultation
  • Commentez avec la communauté
    scientifique
  • Recevez des notifications de mise à jour
    de vos sujets favoris
Copyright Carmin.tv 2024
En poursuivant votre navigation sur ce site, vous acceptez l'utilisation de cookies pour améliorer votre expérience. En savoir plus sur notre politique de confidentialité.
Accepter
Donner son avis