Introducing string field theory from a geometrical perspective
De Harold Erbin
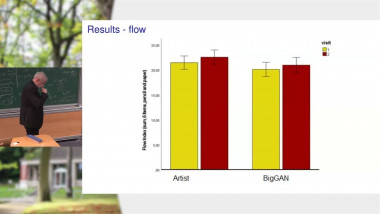
String field theory (SFT) is a second-quantized version of string theory: it provides an explicit regularization of all amplitudes and allows using all the standard techniques from QFT. In this talk, I will explain how SFT is constructed from the data of a 2d CFT (defining the spacetime background) and a decomposition of the moduli space of Riemann surfaces. The latter is background independent and determines a geometrical BV algebra, which implies that the SFT action is a solution of the BV master equation. It also induces an L-infinity algebra, which characterizes the form of the action and of its gauge symmetries. To conclude, I will exemplify this interplay between geometry and field theory by showing how neural networks can be used to construct data on the moduli spaces and compute the closed string tachyon potential.