PDMPs and Integrals PDMPs in risk theory and QMC integration II
Also appears in collection : Jean-Morlet Chair 2020 - Research School: Quasi-Monte Carlo Methods and Applications / Chaire Jean-Morlet 2020 - Ecole: Méthode de quasi-Monte-Carlo et applications
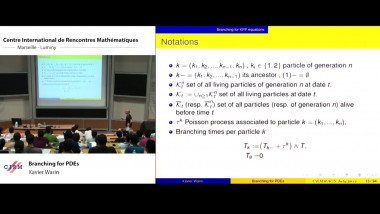
This talk will give an overview on the usage of piecewise deterministic Markov processes for risk theoretic modeling and the application of QMC integration in this framework. This class of processes includes several common risk models and their generalizations. In this field, many objects of interest such as ruin probabilities, penalty functions or expected dividend payments are typically studied by means of associated integro-differential equations. Unfortunately, only particular parameter constellations allow for closed form solutions such that in general one needs to rely on numerical methods. Instead of studying these associated integro-differential equations, we adapt the problem in a way that allows us to apply deterministic numerical integration algorithms such as QMC rules.