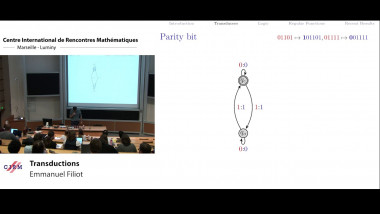
Basics on affine Grassmanianns
By Timo Richarz
Also appears in collection : Buildings and Affine Grassmannians / Immeubles et grassmanniennes affines
The aim is to give an introduction to the basic theory of affine Grassmannians and affine flag varieties. We put special emphasis on the utility of dynamic methods in sense of Drinfeld [D], and the utility of non-constant group schemes. We plan to adress the following aspects: • Affine Grassmannians as moduli spaces of G-bundles, and as quotients of loop groups ; • Cell decompositions of affine Grassmannians and affine flag varieties via dynamic methods: Iwahori, Cartan and Iwasawa decompositions ; • Schubert varieties, Demazure resolutions, Convolution morphisms, Combinatorial structures ; • Moduli spaces of G-bundles with level structure versus bundles under non-constant group schemes ; • Beilinson-Drinfeld type deformations of affine Grassmannians ; • Relation to the local geometry of moduli spaces of Drinfeld shtukas and Shimura varieties.