Carmin.tv

Mathematics
and Interactions

Please leave your feedback in order for us to improve your experience !
Not Only Scalar Curvature Seminar
74 videos

Not Only Scalar Curvature Seminar

Geometric structures and discrete group actions / Structures géométriques et actions de groupes discrets
4 videos

Geometric structures and discrete group actions / Structures géométriques et actions de groupes discrets

Misha Gromov : Mathematical Description of Biological Structures
4 videos

Misha Gromov : Mathematical Description of Biological Structures

Applications of NonCommutative Geometry to Gauge Theories, Field Theories, and Quantum Space-Time / Applications de la Géométrie Non Commutative aux Théories de Jauge, à la Théorie des Champs et aux Espaces-Temps Quantiques
5 videos

Applications of NonCommutative Geometry to Gauge Theories, Field Theories, and Quantum Space-Time / Applications de la Géométrie Non Commutative aux Théories de Jauge, à la Théorie des Champs et aux Espaces-Temps Quantiques

All the collections
CIMPA
CIRM
IHES
IHP
LMR
SMF
All the institutions
Combinatorics and Arithmetic for Physics: special days 2023

Collection Combinatorics and Arithmetic for Physics: special days 2023

Organizer(s) Gérard H. E. DUCHAMP, Maxim KONTSEVICH, Gleb KOSHEVOY, Sergei NECHAEV and Karol A. PENSON
Date(s) 15/11/2023 - 17/11/2023
linked URL https://www-lipn.univ-paris13.fr/~duchamp/Conferences/CAP10_2023.html
00:00:00 / 00:00:00
4 27

On Manin–Schechtman orders related to directed graphs

By Gleb Koshevoy

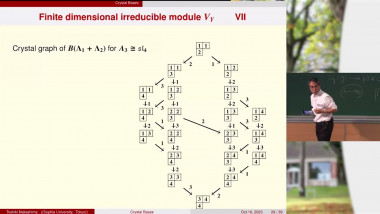
Studying higher Zamolodchikov equations, in 1989 Manin and Schechtman introduced the notion of a higher Bruhat order on the d-element subsets of a set $[n] = \{1, 2, . . . , n}$. We consider a wider model, involving the so-called convex order on certain path systems in an acyclic directed graph, introduce local transformations, or flips, on such orders and establish a generalization of the Manin-Schechtman results. This is a joint work with V.Danilov and A. Karzanov.

Information about the video

  • Date of recording 15/11/2023
  • Date of publication 16/11/2023
  • Institution IHES
  • Licence CC BY-NC-ND
  • Language English
  • Audience Researchers
  • Format MP4

Domain(s)

Last related questions on MathOverflow

You have to connect your Carmin.tv account with mathoverflow to add question

Ask a question on MathOverflow




Register

  • Bookmark videos
  • Add videos to see later &
    keep your browsing history
  • Comment with the scientific
    community
  • Get notification updates
    for your favorite subjects
Copyright Carmin.tv 2025
By browsing our website, you accept the use of cookies to improve your experience. Find out more about our privacy policy.
Approve
Give feedback