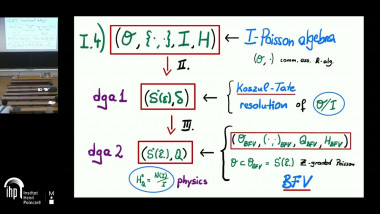
A geometrisation of N-manifolds of degree $n$
Lie $2$-algebroids are geometrised by linear Courant algebroids, while symplectic Lie $2$-algebroids correspond to mere Courant algebroids.
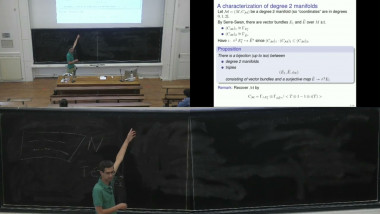
This talk begins by explaining these correspondences due to Li-Bland, Severa and Roytenberg, by establishing the underlying equivalence between [2]-manifolds and metric double vector bundles. The latter yields a dictionary between graded geometric structures on [2]-manifolds, like homological vector fields, Poisson and symplectic structures, and corresponding 'classical geometric' structures on the corresponding metric double vector bundles.
Metric double vector bundles dualise to double vector bundles equipped with a (signed) involution. The latter can then be understood as $S2$-symmetric double vector bundles -- recovering Pradines' 'inverse' symmetric double vector bundles. Similarly, positively graded manifold of arbitrary degree $n$ are equivalent to $n$-fold vector bundles equipped with a (signed) $Sn$-symmetry. This talk explains more precisely how symmetric $n$-fold vector bundle cocycles are the same objects as [$n$]-manifold cocycles, and how symmetric vector bundles, which are indexed by $n$-cube categories, provide a new and insightful point of view on (positively) graded geometry.
This is the groundwork for understanding a possible geometrisation of Lie $n$-algebroids, like VB-Courant algebroids geometrise Lie $2$-algebroids, and Lie algebroids geometrise Lie $1$-algebroids.
This work is partly joint with Malte Heuer.