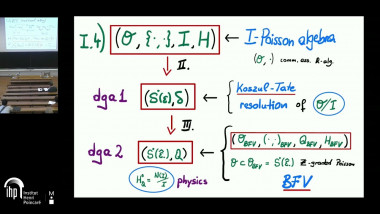
A classical theorem of Van Est relates the differentiable cohomology of a Lie group to the cohomology of its Lie algebra. I will discuss a version of this result for homotopy-theoretic variants of Lie group(oid)s, such as the string group. This relates the derived category of representations of such a groupoid to the derived category of representations of its Lie algebroid. In particular, this relies on a version of Koszul duality for Lie algebroids.
De Pavel Mnev
De Jae-Suk Park
De Ruben Louis
De Thomas Strobl
De Hsuan-Yi Liao
De Christian Blohmann
De Tilmann Wurzbacher
De Owen Gwilliam
De Adrien Brochier
De Jérémie Pierard de Maujouy
De Pavol Severa
De Roberta Anna Iseppi
De Alain Connes
De Teresa Krick
De Teresa Krick
