De Marco Zambon
Courant algebroids are certain objects in Lie theory that are used to define, for instance, Dirac structures and generalized complex structures.
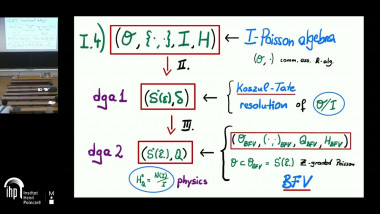
We will use the correspondence between degree 2 symplectic manifolds and Courant algebroids, due to Roytenberg, to approach the reduction of Courant algebroids using graded geometry. For this purpose we will consider both graded coisotropic submanifolds and a graded version of moment maps. The resulting reduction procedure, in a particular case, recovers the work of Bursztyn-Cavalcanti-Gualtieri around 2007. This talk is based on joint work with Bursztyn, Cattaneo and Metha.
De Pavel Mnev
De Jae-Suk Park
De Ruben Louis
De Thomas Strobl
De Hsuan-Yi Liao
De Christian Blohmann
De Tilmann Wurzbacher
De Owen Gwilliam
De Adrien Brochier
De Jérémie Pierard de Maujouy
De Pavol Severa
De Roberta Anna Iseppi
De Alain Connes
De Teresa Krick
De Teresa Krick
