2023 - T2 - WS3 - Dg-manifolds in geometry and physics

Collection 2023 - T2 - WS3 - Dg-manifolds in geometry and physics

Organizer(s) Hélein, Frédéric ; Ginot, Grégory ; Laurent-Gengoux, Camille

Date(s) 03/07/2023 - 07/07/2023

linked URL https://indico.math.cnrs.fr/event/7885/

00:00:00 / 00:00:00

9 21

Reduction of Courant algebroids via graded manifolds

By Marco Zambon

Courant algebroids are certain objects in Lie theory that are used to define, for instance, Dirac structures and generalized complex structures.

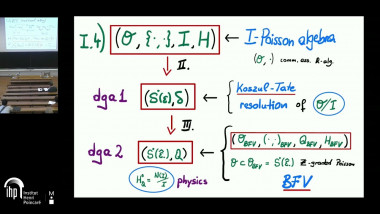
We will use the correspondence between degree 2 symplectic manifolds and Courant algebroids, due to Roytenberg, to approach the reduction of Courant algebroids using graded geometry. For this purpose we will consider both graded coisotropic submanifolds and a graded version of moment maps. The resulting reduction procedure, in a particular case, recovers the work of Bursztyn-Cavalcanti-Gualtieri around 2007. This talk is based on joint work with Bursztyn, Cattaneo and Metha.

Information about the video

Date of recording 04/07/2023
Date of publication 06/07/2023
Institution IHP
Licence CC BY-NC-ND
Language English
Audience Researchers
Director(s) Alexandre Duplessis
Format MP4
Venue IHP - Hermite Amphitheater

Citation data

DOI 10.57987/IHP.2023.T2.WS3.009
Cite this video Zambon, Marco (04/07/2023). Reduction of Courant algebroids via graded manifolds. IHP. Audiovisual resource. DOI: 10.57987/IHP.2023.T2.WS3.009
URL https://dx.doi.org/10.57987/IHP.2023.T2.WS3.009

Domain(s)

Symplectic Geometry

Last related questions on MathOverflow

You have to connect your Carmin.tv account with mathoverflow to add question

Ask a question on MathOverflow

All the collection videos

45:46

published on July 6, 2023

Differentiation of simplicial manifolds

By Leonid Ryvkin

58:42

published on July 6, 2023

Examples of bulk-boundary correspondences of field theories as BV pushforwards

By Pavel Mnev

51:33

published on July 6, 2023

Grothendieck-Galois theories over symmetric monoidal categories

By Jae-Suk Park

33:19

published on July 6, 2023

Lie-Rinehart algebras as acyclic dg-manifolds and geometric applications

By Ruben Louis

47:33

published on July 6, 2023

Arborescent Koszul-Tate resolutions and BFV for singular coisotropic reductions

By Thomas Strobl

52:23

published on July 6, 2023

Dg bundles with some applications

By Oleksii Kotov

51:51

published on July 6, 2023

Homotopy fiber product and dg manifolds of finite positive amplitudes

By Hsuan-Yi Liao

58:58

published on July 6, 2023

A geometrisation of N-manifolds of degree $n$

By Madeleine Jotz

54:22

published on July 6, 2023

Reduction of Courant algebroids via graded manifolds

By Marco Zambon

01:06:01

published on July 6, 2023

The Van Est isomorphism for higher stacks

By Joost-Jakob Nuiten

29:38

published on July 6, 2023

Dendroidal ∞-operads

By Francesca Pratali

51:52

published on July 6, 2023

Derived Poisson structures

By Jonathan Pridham

01:03:07

published on July 6, 2023

The differentiation of higher elastic diffeological groupoids

By Christian Blohmann

01:00:14

published on July 6, 2023

Some remarks on multisymplectic geometry (or from Volterra to "higher" structures)

By Tilmann Wurzbacher

50:22

published on July 6, 2023

BV formalism in the infinite dimensional setting

By Kasia Rejzner

54:55

published on July 6, 2023

4-dimensional gauge theories and their holomorphic twists

By Owen Gwilliam

54:45

published on July 6, 2023

Higher differential geometry and symplectic structure

By Chenchang Zhu

01:01:01

published on July 25, 2023

Quantum exponentiation of Hamiltonian Poisson varieties

By Adrien Brochier

27:33

published on July 7, 2023

Generalised Frame Bundles and Einstein's Equation

By Jérémie Pierard de Maujouy

51:13

published on July 7, 2023

Fried's conjecture in quantum field theory

By Michele Schiavina

53:46

published on July 25, 2023

Lie bialgebroids and double groupoids in the braided world

By Pavol Severa

Copyright Carmin.tv 2025

Give feedback