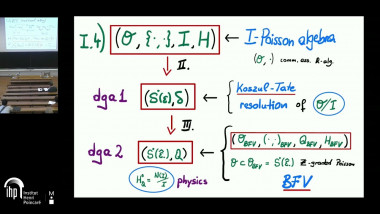
Let I be an ideal in a commutative (associative) algebra O. Starting from a resolution of O/I as an O-module, we construct a Koszul-Tate resolution for this quotient, i.e.\ a graded symmetric algebra over O with a differential which provides simultaneously a resolution as an O-module. This algebra resolution has the beautiful structure of a forest of decorated trees and is related to an A-infinity algebra on the original module resolution. Considering O to be a Poisson algebra and I a finitely generated Poisson subalgebra, we use the above construction to obtain the corresponding BFV formulation. Its cohomology at degree zero is proven to coincide with the reduced Poisson algebra N(I)/I, where N(I) is the normaliser of I inside O, thus generalising ordinary coisotropic reduction to the singular setting. As an illustration we use the example where O consists of functions on T^*(\R^3) and I is the ideal generated by angular momenta.
This is joint work with Aliaksandr Hancharuk and, in part, with Camille Laurent-Gengoux.
By Pavel Mnev
By Jae-Suk Park
By Ruben Louis
By Thomas Strobl
By Hsuan-Yi Liao
By Christian Blohmann
By Tilmann Wurzbacher
By Owen Gwilliam
By Adrien Brochier
By Jérémie Pierard de Maujouy
By Pavol Severa
By Roberta Anna Iseppi
By Alain Connes
By Teresa Krick
By Teresa Krick
