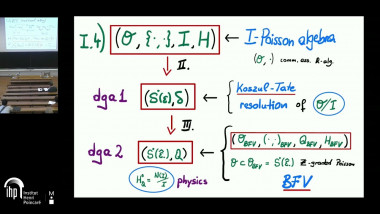
First, I will review the notion of elastic diffeological spaces, on which there is a natural Cartan calculus. I will define diffeological Lie algebroids, show how they arise from elastic diffeological groupoids, and give their dual description as ringed diffeological spaces with a homological vector field. Then I will explain how to generalize this construction to higher diffeological groupoids, which yields a simple universal formula given by the coend of a cosimplicial-simplicial object in ringed diffeological spaces with a homological vector field. The project is motivated by geometric deformation theory, and is joint work with Lory Kadiyan.
By Pavel Mnev
By Jae-Suk Park
By Ruben Louis
By Thomas Strobl
By Hsuan-Yi Liao
By Christian Blohmann
By Tilmann Wurzbacher
By Owen Gwilliam
By Adrien Brochier
By Jérémie Pierard de Maujouy
By Pavol Severa
By Roberta Anna Iseppi
By Alain Connes
By Teresa Krick
By Teresa Krick
