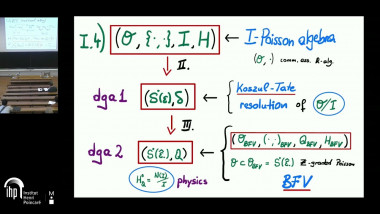
A main motivation for developing derived differential geometry is to deal with singularities arising from zero loci or intersections of submanifolds. Both zero loci and intersections can be considered as fiber products of manifolds which may not be manifolds. To deal with this issue, we extend the category of differentiable manifolds to the category of dg manifolds of finite positive amplitudes in which "homotopy fiber products" exist. In this talk, I would like to explain properties of this larger category (it is a category of fibrant objects) and our construction of homotopy fiber products of manifolds. The talk is mainly based on a joint work with Kai Behrend and Ping Xu.
By Pavel Mnev
By Jae-Suk Park
By Ruben Louis
By Thomas Strobl
By Hsuan-Yi Liao
By Christian Blohmann
By Tilmann Wurzbacher
By Owen Gwilliam
By Adrien Brochier
By Jérémie Pierard de Maujouy
By Pavol Severa
