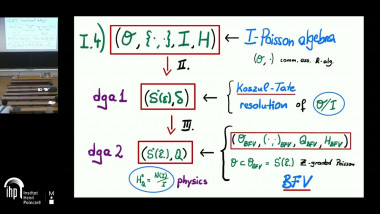
Let I be an ideal in a commutative (associative) algebra O. Starting from a resolution of O/I as an O-module, we construct a Koszul-Tate resolution for this quotient, i.e.\ a graded symmetric algebra over O with a differential which provides simultaneously a resolution as an O-module. This algebra resolution has the beautiful structure of a forest of decorated trees and is related to an A-infinity algebra on the original module resolution. Considering O to be a Poisson algebra and I a finitely generated Poisson subalgebra, we use the above construction to obtain the corresponding BFV formulation. Its cohomology at degree zero is proven to coincide with the reduced Poisson algebra N(I)/I, where N(I) is the normaliser of I inside O, thus generalising ordinary coisotropic reduction to the singular setting. As an illustration we use the example where O consists of functions on T^*(\R^3) and I is the ideal generated by angular momenta.
This is joint work with Aliaksandr Hancharuk and, in part, with Camille Laurent-Gengoux.
De Pavel Mnev
De Jae-Suk Park
De Ruben Louis
De Thomas Strobl
De Hsuan-Yi Liao
De Christian Blohmann
De Tilmann Wurzbacher
De Owen Gwilliam
De Adrien Brochier
De Jérémie Pierard de Maujouy
De Pavol Severa
De Roberta Anna Iseppi
De Alain Connes
De Teresa Krick
De Teresa Krick
