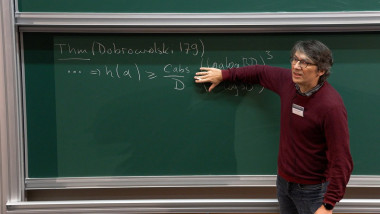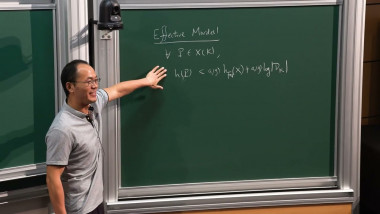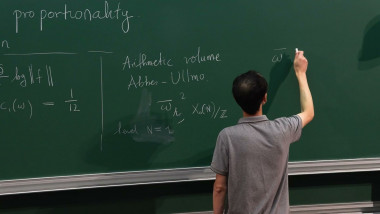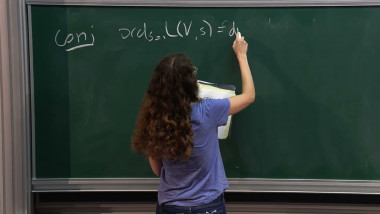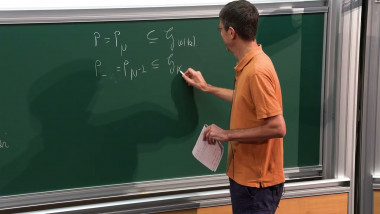The Arithmetic of Power Series and Applications to Irrationality
By Yunqing Tang
We will discuss a new approach to prove irrationality of certain periods, including the value at 2 of the Dirichlet L-function associated to the primitive quadratic character with conductor -3. Our method uses rational approximations from the literature and we develop a new framework to make use of these approximations. The key ingredient is an arithmetic holonomy theorem built upon earlier work by André, Bost, Charles (and others) on arithmetic algebraization theorems via Arakelov theory. This is joint work with Frank Calegari and Vesselin Dimitrov.