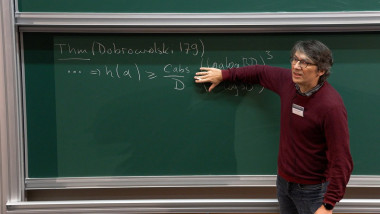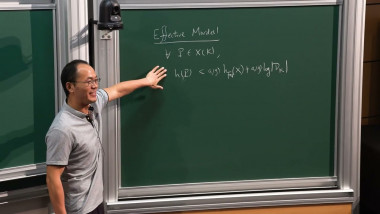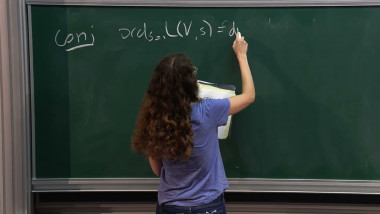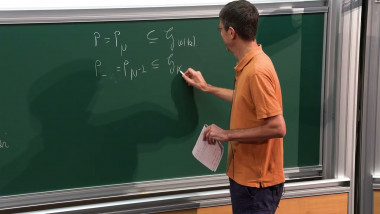The Bombieri-Dwork conjecture predicts that an irreducible differential operator with a G-function solution comes from geometry, that is, encodes how periods vary in a pencil of algebraic varieties. This conjecture is completely open for operators of order at least 2. At the beginning of the 90s, Dwork proposed a strategy to establish the conjecture for G-operators of order 2, which would consist in proving that they are all pullbacks by a correspondence of some Gauss's hypergeometric differential operator. Sporadic counterexamples to this expectation were found by Kraamer (1996) and Bouw-Möller (2010). I will present a joint work with Josh Lam and Yichen Qin where we prove that most G-operators of order 2 coming from geometry are not pullbacks of hypergeometric differential operators. A key ingredient to construct infinitely many counterexamples will be a theme dear to Emmanuel: the André-Pink-Zannier conjecture for Shimura varieties, in the cases recently established by Richard and Yafaev.