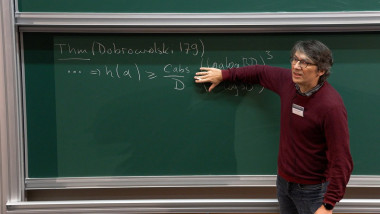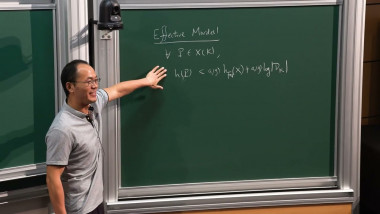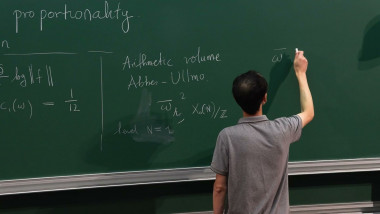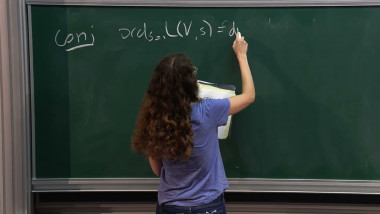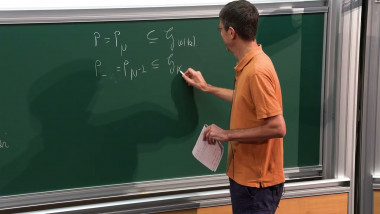Arithmetic and Diophantine Geometry, via Ergodic Theory and o-minimality

Collection Arithmetic and Diophantine Geometry, via Ergodic Theory and o-minimality

Organizer(s) Ahmed Abbes, Jennifer Balakrishnan, Ziyang Gao, Marc Hindry, Fanny Kassel, Bruno Klingler, Yuri Tschinkel

Date(s) 08/09/2025 - 12/09/2025

linked URL https://indico.math.cnrs.fr/event/13164/

00:00:00 / 00:00:00

13 20

Convolution and Square on Abelian Groups

By Yves Benoist

We will construct functions on finite abelian groups whose convolution square is proportional to their square. For that, we will interpret the abelian group as a subgroup of an abelian variety with complex multiplication, and use the modularity properties of their theta functions.

Information about the video

Date of recording 10/09/2025
Date of publication 16/09/2025
Institution IHES
Language English
Audience Researchers
Format MP4

Domain(s)

Last related questions on MathOverflow

You have to connect your Carmin.tv account with mathoverflow to add question

Ask a question on MathOverflow

All the collection videos

01:06:15

published on September 12, 2025

The Arithmetic of Power Series and Applications to Irrationality

By Yunqing Tang

01:11:46

published on September 12, 2025

Integral points and affineness in Arakelov geometry

By François Charles

01:04:31

published on September 12, 2025

Infinitely Many Non-hypergeometric Local Systems

By Javier Fresán

01:07:45

published on September 16, 2025

The Dynamical Schinzel-Zassenhaus Conjecture and the Transfinite Diameter of Trees

By Philipp Habegger

01:04:16

published on October 6, 2025

Elliptic surfaces, Equidistribution, and Bifurcations

By Laura Demarco

01:08:58

published on September 16, 2025

Baily-Borel Compactifications of Period Images and the b-semiampleness Conjecture

By Benjamin Bakker

01:11:18

published on September 16, 2025

Applications of Unlikely Intersections to Integral Geometry

By David Urbanik

01:02:37

published on September 16, 2025

A Tribute to Emmanuel's Contributions to the Zilber–Pink Conjecture

By Gregorio Baldi

01:06:57

published on September 16, 2025

Determinant Values on Irrational Lattices

By Hee Oh

01:07:33

published on September 16, 2025

Higher property T, Banach Representations and Applications

By Uri Bader

01:13:56

published on September 16, 2025

Convolution and Square on Abelian Groups

By Yves Benoist

01:05:44

published on September 17, 2025

A Quantitative Version of the Uniform Mordell Conjecture

By Xinyi Yuan

01:07:05

published on September 17, 2025

Heights of Ceresa and Gross-Schoen Cycles

By Shouwu Zhang

01:06:52

published on September 17, 2025

Proportionality and the arithmetic volumes of Shimura varieties and the moduli of Shtukas

By Wei Zhang

01:03:32

published on September 17, 2025

On the Bloch–Kato Conjecture for some four-dimensional symplectic Galois representations

By Naomi Sweeting

01:03:04

published on September 18, 2025

On two mod p period maps: Ekedahl--Oort and fine Deligne--Lusztig stratifications

By Fabrizio Andreatta

01:06:27

published on September 18, 2025

Tate locus - conjectures and results

By Anna Cadoret

59:09

published on September 18, 2025

A split version of the mixing conjecture and applications

By Philippe Michel

Copyright Carmin.tv 2025

Give feedback