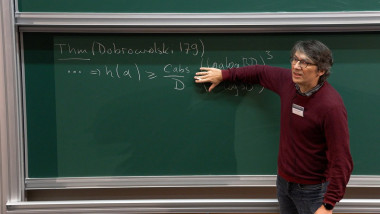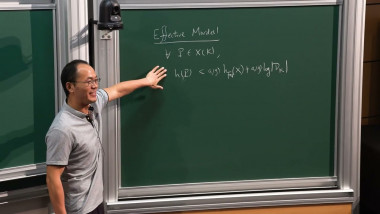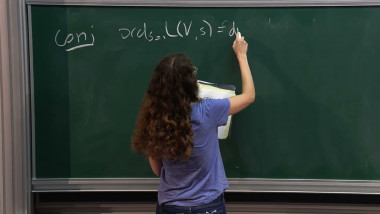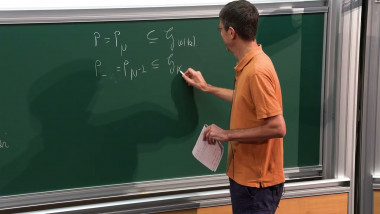Arithmetic and Diophantine Geometry, via Ergodic Theory and o-minimality

Collection Arithmetic and Diophantine Geometry, via Ergodic Theory and o-minimality

Organizer(s) Ahmed Abbes, Jennifer Balakrishnan, Ziyang Gao, Marc Hindry, Fanny Kassel, Bruno Klingler, Yuri Tschinkel

Date(s) 08/09/2025 - 12/09/2025

linked URL https://indico.math.cnrs.fr/event/13164/

00:00:00 / 00:00:00

7 20

Elliptic surfaces, Equidistribution, and Bifurcations

By Laura Demarco

In joint work with Mavraki a few years ago, we studied the arithmetic intersection numbers of sections of elliptic surfaces, defined over number fields. One consequence was a Bogomolov-type extension (and new proof) of a theorem of Barroero and Capuano, addressing a case of the Zilber Pink conjectures. I will describe the underlying geometric features of this problem and formulate related open questions about families of maps (dynamical systems) on $P^1$.

Information about the video

Date of recording 09/09/2025
Date of publication 06/10/2025
Institution IHES
Language English
Audience Researchers
Format MP4

Domain(s)

Last related questions on MathOverflow

You have to connect your Carmin.tv account with mathoverflow to add question

Ask a question on MathOverflow

All the collection videos

01:06:15

published on September 12, 2025

The Arithmetic of Power Series and Applications to Irrationality

By Yunqing Tang

01:11:46

published on September 12, 2025

Integral points and affineness in Arakelov geometry

By François Charles

01:04:31

published on September 12, 2025

Infinitely Many Non-hypergeometric Local Systems

By Javier Fresán

01:07:45

published on September 16, 2025

The Dynamical Schinzel-Zassenhaus Conjecture and the Transfinite Diameter of Trees

By Philipp Habegger

01:04:16

published on October 6, 2025

Elliptic surfaces, Equidistribution, and Bifurcations

By Laura Demarco

01:08:58

published on September 16, 2025

Baily-Borel Compactifications of Period Images and the b-semiampleness Conjecture

By Benjamin Bakker

01:11:18

published on September 16, 2025

Applications of Unlikely Intersections to Integral Geometry

By David Urbanik

01:02:37

published on September 16, 2025

A Tribute to Emmanuel's Contributions to the Zilber–Pink Conjecture

By Gregorio Baldi

01:06:57

published on September 16, 2025

Determinant Values on Irrational Lattices

By Hee Oh

01:07:33

published on September 16, 2025

Higher property T, Banach Representations and Applications

By Uri Bader

01:13:56

published on September 16, 2025

Convolution and Square on Abelian Groups

By Yves Benoist

01:05:44

published on September 17, 2025

A Quantitative Version of the Uniform Mordell Conjecture

By Xinyi Yuan

01:07:05

published on September 17, 2025

Heights of Ceresa and Gross-Schoen Cycles

By Shouwu Zhang

01:06:52

published on September 17, 2025

Proportionality and the arithmetic volumes of Shimura varieties and the moduli of Shtukas

By Wei Zhang

01:03:32

published on September 17, 2025

On the Bloch–Kato Conjecture for some four-dimensional symplectic Galois representations

By Naomi Sweeting

01:03:04

published on September 18, 2025

On two mod p period maps: Ekedahl--Oort and fine Deligne--Lusztig stratifications

By Fabrizio Andreatta

01:06:27

published on September 18, 2025

Tate locus - conjectures and results

By Anna Cadoret

59:09

published on September 18, 2025

A split version of the mixing conjecture and applications

By Philippe Michel

Copyright Carmin.tv 2025

Give feedback