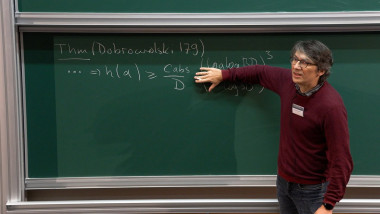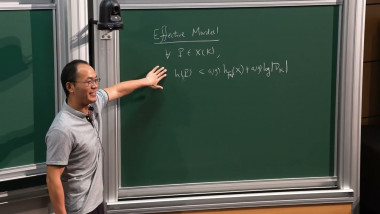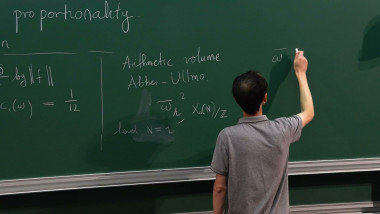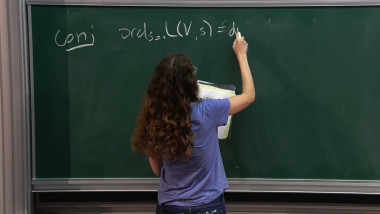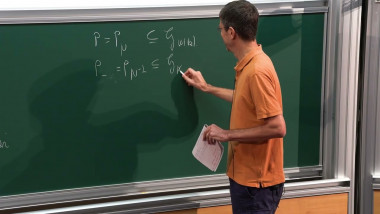Carmin.tv

Mathematics
and Interactions

Please leave your feedback in order for us to improve your experience !
13e Séminaire Itzykson : Bootstrap conforme et géométrie spectrale
3 videos

13e Séminaire Itzykson : Bootstrap conforme et géométrie spectrale

Exposition Laurent Schwartz
4 videos

Exposition Laurent Schwartz

Open science put to the test of rights and duties: mathematicians and librarians, let's educate ours / Science ouverte a l'épreuve des droits et devoirs : mathématiciens-nes et bibliothécaires, (in)formons-nous
8 videos

Open science put to the test of rights and duties: mathematicians and librarians, let's educate ours / Science ouverte a l'épreuve des droits et devoirs : mathématiciens-nes et bibliothécaires, (in)formons-nous

Conférences grand public MathEnVille
1 videos

Conférences grand public MathEnVille

All the collections
CIMPA
CIRM
IHES
IHP
Institut Fourier
LMR
SMF
All the institutions
Arithmetic and Diophantine Geometry, via Ergodic Theory and o-minimality

Collection Arithmetic and Diophantine Geometry, via Ergodic Theory and o-minimality

Organizer(s) Ahmed Abbes, Jennifer Balakrishnan, Ziyang Gao, Marc Hindry, Fanny Kassel, Bruno Klingler, Yuri Tschinkel
Date(s) 08/09/2025 - 12/09/2025
linked URL https://indico.math.cnrs.fr/event/13164/
00:00:00 / 00:00:00
19 20

Tate locus - conjectures and results

By Anna Cadoret

Let k be a field and X a geometrically connected variety over k. The Tate or degeneracy locus of a l-adic local system on X is the etale counterpart of the Hodge locus of a VHS. While in the last decade tremendous progresses have been made in understanding the latter thanks to, in particular, techniques from o-minimality, much less is known about the former. I will review the main conjectures (and mention briefly some applications) about this locus when k is a number field, and explain what we can currently prove. This should include joint works with Jakob Stix and Akio Tamagawa.

Information about the video

  • Date of recording 12/09/2025
  • Date of publication 18/09/2025
  • Institution IHES
  • Language English
  • Audience Researchers
  • Format MP4

Domain(s)

Last related questions on MathOverflow

You have to connect your Carmin.tv account with mathoverflow to add question

Ask a question on MathOverflow




Register

  • Bookmark videos
  • Add videos to see later &
    keep your browsing history
  • Comment with the scientific
    community
  • Get notification updates
    for your favorite subjects
Copyright Carmin.tv 2025
By browsing our website, you accept the use of cookies to improve your experience. Find out more about our privacy policy.
Approve
Give feedback