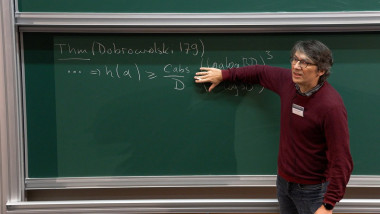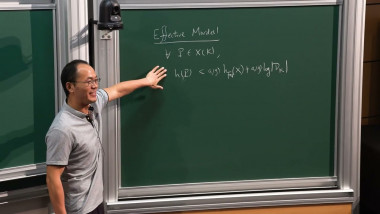Carmin.tv

Mathematics
and Interactions

Please leave your feedback in order for us to improve your experience !
13e Séminaire Itzykson : Bootstrap conforme et géométrie spectrale
3 videos

13e Séminaire Itzykson : Bootstrap conforme et géométrie spectrale

Exposition Laurent Schwartz
4 videos

Exposition Laurent Schwartz

Open science put to the test of rights and duties: mathematicians and librarians, let's educate ours / Science ouverte a l'épreuve des droits et devoirs : mathématiciens-nes et bibliothécaires, (in)formons-nous
8 videos

Open science put to the test of rights and duties: mathematicians and librarians, let's educate ours / Science ouverte a l'épreuve des droits et devoirs : mathématiciens-nes et bibliothécaires, (in)formons-nous

Conférences grand public MathEnVille
1 videos

Conférences grand public MathEnVille

All the collections
CIMPA
CIRM
IHES
IHP
Institut Fourier
LMR
SMF
All the institutions
Arithmetic and Diophantine Geometry, via Ergodic Theory and o-minimality

Collection Arithmetic and Diophantine Geometry, via Ergodic Theory and o-minimality

Organizer(s) Ahmed Abbes, Jennifer Balakrishnan, Ziyang Gao, Marc Hindry, Fanny Kassel, Bruno Klingler, Yuri Tschinkel
Date(s) 08/09/2025 - 12/09/2025
linked URL https://indico.math.cnrs.fr/event/13164/
00:00:00 / 00:00:00
8 20

Baily-Borel Compactifications of Period Images and the b-semiampleness Conjecture

By Benjamin Bakker

We address two questions related to the semiampleness of line bundles arising from Hodge theory. First, we prove there is a functorial compactification of the image of a period map of a polarizable integral pure variation of Hodge structures for which a natural line bundle extends amply. This generalizes the Baily--Borel compactification of a Shimura variety, and for instance produces Baily--Borel type compactifications of moduli spaces of Calabi--Yau varieties. We prove more generally that the Hodge bundle of a Calabi--Yau variation of Hodge structures is semiample subject to some extra conditions, and as our second result deduce the b-semiampleness conjecture of Prokhorov--Shokurov. The semiampleness results crucially use o-minimal GAGA, and the deduction of the b-semiampleness conjecture uses work of Ambro and results of Koll\'ar on minimal lc centers to verify the extra conditions geometrically. This is joint work with S. Filipazzi, M. Mauri, and J. Tsimerman.

Information about the video

  • Date of recording 09/09/2025
  • Date of publication 16/09/2025
  • Institution IHES
  • Language English
  • Audience Researchers
  • Format MP4

Domain(s)

Last related questions on MathOverflow

You have to connect your Carmin.tv account with mathoverflow to add question

Ask a question on MathOverflow




Register

  • Bookmark videos
  • Add videos to see later &
    keep your browsing history
  • Comment with the scientific
    community
  • Get notification updates
    for your favorite subjects
Copyright Carmin.tv 2025
By browsing our website, you accept the use of cookies to improve your experience. Find out more about our privacy policy.
Approve
Give feedback