
Fukaya categories associated with graded surfaces and gentle algebras 1
By Claire Amiot
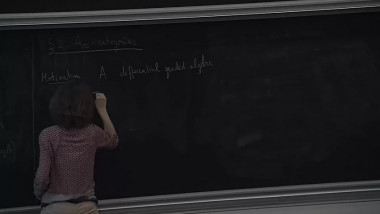
Fukaya categories associated with graded surfaces and gentle algebras 2
By Claire Amiot
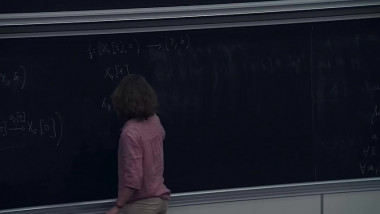
Fukaya categories associated with graded surfaces and gentle algebras 3
By Claire Amiot
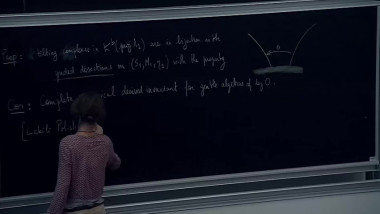
Fukaya categories associated with graded surfaces and gentle algebras 4
By Claire Amiot

Higgs bundles for Hecke eigensheaves in rank 2 and genus 2
By Carlos Simpson











