Appears in collection : Combinatorics and Arithmetic for Physics: special days 2023

Poisson brackets on $\mathbb R^n$ are bi-linear skew-symmetric bi-derivations of $C^\infty(\mathbb R^n)$ satisfying the Jacobi identity, generalizing the canonical Poisson bracket from classical mechanics. Some interesting classes of examples are the Nambu–Poisson brackets defined via the Jacobian determinant with $n − 2$ arbitrary functions, the quadratic and cubic R-matrix Poisson brackets associated with Lie algebras, and all the bi-vector fields on $\mathbb R^2$.

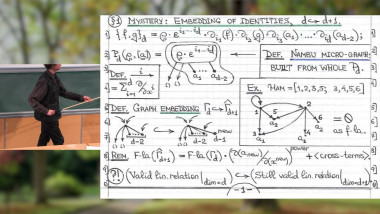
While the flow of an arbitrary vector field on $\mathbb R^n$ induces a (cohomologically) trivial infinitesimal deformation of a Poisson bracket, some brackets admit nontrivial deformations. To infinitesimally deform any Poisson structure on $\mathbb R^n$, M. Kontsevich introduced an infinite family of formulas, depending nonlinearly and differential-polynomially on the Poisson bracket coefficients. Every such deformation formula is constructed from a linear combination of graphs that forms a cocycle in the graph complex, and graph coboundaries are naturally mapped to cohomologically trivial deformations. Nonzero graph cohomology classes (of which the first example is the tetrahedron) are expected to deform some Poisson bracket nontrivially, but finding an example of this kind is an open problem since 1996.

We illustrate this story in a presentation of the newly developed software package gcaops (Graph Complex Action on Poisson Structures) for SageMath, which is presently used to expand the class of interesting non-examples.

After vigorous computation, the (classes of) vector fields associated with the respective Poisson coboundaries are produced explicitly, with short defining formulas and directed graph representations.

This talk is based on a part of my Ph.D. dissertation, which was supervised by A.V. Kiselev and D. van Straten