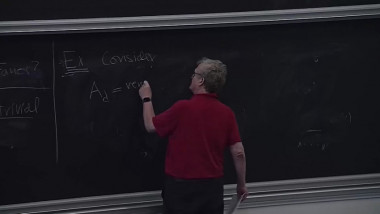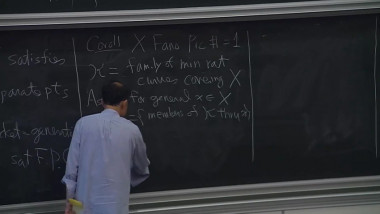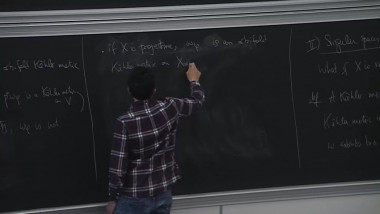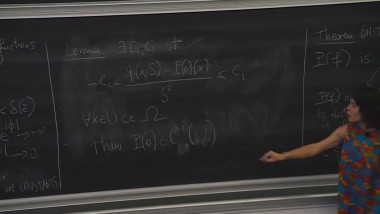We say that the formal principle with convergence holds for a compact complex submanifold A in a complex manifold X, if any formal isomorphism between the formal neighborhood of A in X and that of another complex submanifold A′ in another complex manifold X′ always converges, namely, the formal isomorphism can be extended to a biholomorphic map between suitable neighborhoods. Hirschowitz and Commichau-Grauert showed that the formal principle with convergence holds if the normal bundle of the submanifold is sufficiently positive. We discuss the problem when the normal bundle is only weakly positive, but the submanifold satisfies certain geometric conditions. Our main interest is when the submanifold is a general minimal rational curve in a uniruled projective manifold, such as a general line on a rational homogeneous space or a projective hypersurface of low degree.
By Thomas Peternell
By Robert Berman
By Gergerly Bérczi
By Simone Diverio
By Mihai Păun
By Jun-Muk Hwang
By Henri Guenancia
By Cinzia Casagrande
By Sébastien Boucksom
By Renaud Detcherry
By Renaud Detcherry
