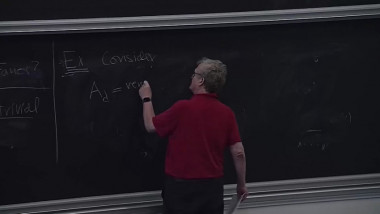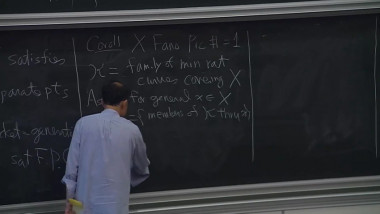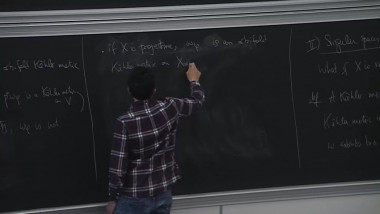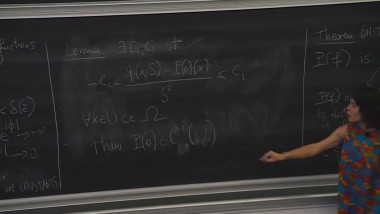By Chenyang Xu
One major new birational geometry problem arising in understanding stable degeneration of varieties, which is the algebraic analogue to the compactness of Kähler-Einstein type metrics, is finite generation for valuations of higher rational rank. In the past a few years, we have established finite generation for minimizing valuations of various functionals, by first showing those minimizers are ‘special’; and then proving any special valuation satisfies finite generation. This raises the question on how ‘special’ valuations are distributed, which still remain to be widely open. In this talk, I will report results and questions along this direction. (Based on joint work with Yuchen Liu and Ziquan Zhuang).
By Thomas Peternell
By Robert Berman
By Gergerly Bérczi
By Simone Diverio
By Mihai Păun
By Jun-Muk Hwang
By Henri Guenancia
By Cinzia Casagrande
By Sébastien Boucksom
By Eugen Hellmann
By Eugen Hellmann
