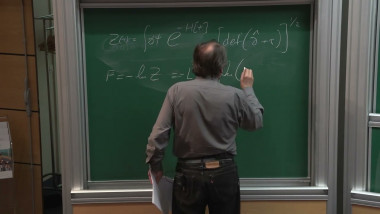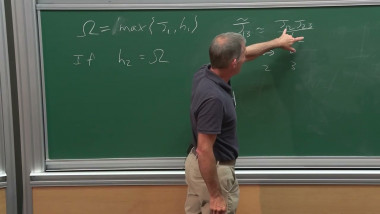Also appears in collection : ECM 2024 Plenary Speakers
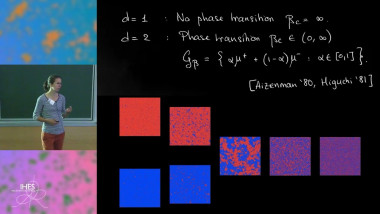
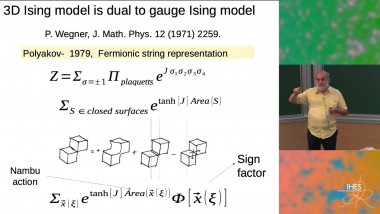
In this talk I will give a panorama of results for the zero-temperature Glauber dynamics of the 3-dimensional (classical) Ising model. It is well known that, with suitable Dobrushin-type boundary conditions, the Boltzmann-Gibbs distribution of a 3d Ising interface at zero temperature coincides with the uniform measure on rhombus tilings of a certain finite (but large) domain D of the plane. In the same situation, the Glauber dynamics can be seen as a Markov evolution on the set of tilings of D. The holy grail conjecture in this respect, suggested by an "anisotropic mean-curvature flow" heuristics for the interface motion, is that the mixing time of the (continuous-time) dynamics is of order $L^{2+o(1)}$, with L the diameter of the domain. I will present old and new results that prove this conjecture under the assumption that the asymptotic limit shape in D (that describes the non-random, typical shape of the Ising interface, for L\to\infty) of has no facets. Based on joint works with B. Laslier, as well as on older works with P. Caputo and F. Martinelli
By Wendelin Werner
By Victor Dotsenko
By Alessandro Giuliani
By Rafael Greenblatt
By Eveliina Peltola
By Giuseppe Mussardo
By Yvan Velenik
By Michele Caselle
By Ara Sedrakyan
By Michael Aizenman
By Jürg Fröhlich , Tom Spencer , Arthur Jaffe , Geoffrey Grimmett , Joel Lebowitz
By Vincent Tassion
By Clément Delcamp
By Clément Delcamp
By Claudio Dappiaggi
By Alexander Strohmaier
